Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 6.1 - Ex. 26
Esboce a região delimitada pelas curvas indicadas e encontre sua área.
Passo 1
Entender como esse gráfico se comporta é o primeiro passo de tudo! . Bom, a função nos diz que todos os valores serão positivos, ou seja, .
Já a função , será uma polinomial de grau 2 com coeficiente angular maior que zero e para cima . Então o nosso graficozinho fica assim:
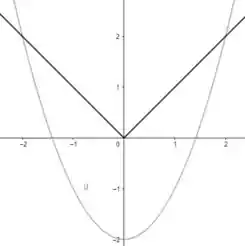
Agora, fazendo a interseção entre as funções, temos:
A gente bate o olho nessa equação e pensa “Hmm, fórmula de bhaskara”, mas o objetivo aqui é facilitar né não? Vamos reescrever a equação:
Logo, , já que não podemos usar valores negativos.
Esse será o nosso intervalo de integração. Agora podemos calcular a área!!
Passo 2
Organizando a integral, temos:
Aqui temos um daqueles caso do Teorema da simetria, portanto
Resolvendo...
Então, isso resultará em:
Prontinho!!