Esboce a região delimitada pelas curvas indicadas. Decida quando integrar em relação a x ou y. Desenhe um retângulo aproximante típico e identifique sua altura e largura. Então, calcule a área da região.

Opa, bora resolver esse problema! O enunciado nos dá a seguinte região:

E pede pra a gente esboçar a região delimitada pelas curvas e calcular a sua área utilizando integral. Pra isso a gente tem que decidir se é melhor integrar com relação a ou !

Bora esboçar a área!

Olha, tem funções que de cara já da pra saber o que ela vai ser. Por exemplo, a função , é uma função polinomial e com coeficiente angular maior que 0, ou seja, para cima.

Já a função , é uma função afim e com coeficiente angular maior que 0, ou seja, crescente.

Porém, não sabemos os pontos de interseção. Vamos descobrir!!

A gente bate o olho nessa equação e pensa “Hmm, fórmula de bhaskara”, mas o objetivo aqui é facilitar né não? Vamos reescrever a equação:

Logo, temos que . Então, o nosso gráfico vai ser desse jeitinho:

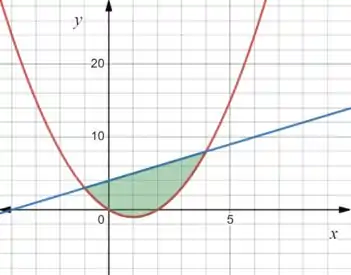
O enunciado não fala qual é o limite integração, mas as próprias curvas dão a dica pra a gente! Queremos descobrir a área em verde! Isso porque é só nessa região que as curvas se interceptam!

Se extrairmos uma parte desse retângulo, vamos ter que a altura será a diferença entre as curvas e a largura será a variação de . Assim:

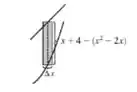
Okay? Agora é só calcularmos a área!!