Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.1 - Ex. 24

Esboce a região delimitada pelas curvas indicadas e encontre sua área.

y = cos ⁡ x , y = 1 - cos ⁡ x , 0 ≤ x ≤ π

Passo 1

Entender como esse gráfico se comporta é o primeiro passo de tudo! . Bom, a função y = cos ⁡ x tem um comportamento especifico sendo positiva em 0 e π .

Já a função y = 1 - cos ⁡ x será a função cosseno, porém com uma unidade a menos, isso significa que ela passará pela origem, diferente da cosseno. Então o nosso graficozinho fica assim:

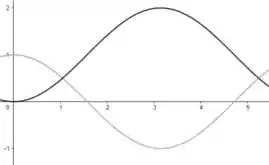
Agora, fazendo a interseção entre as funções, temos:

cos ⁡ x = 1 - cos ⁡ x

2 cos ⁡ x = 1

cos ⁡ x = 1 2

Para o cosseno ser esse valor, o ângulo deve ser x = π 3 . Lembrando que o enunciado nos dá o intervalo de 0 ≤ x ≤ π !!

Esse será o nosso intervalo de integração. Agora podemos calcular a área!!

Passo 2

Organizando a integral, temos:

A = ∫ 0 π 3 [ cos ⁡ x - 1 - cos ⁡ x ] d x + ∫ π 3 π [ 1 - cos ⁡ x - cos ⁡ x ] d x

A = ∫ 0 π 3 [ 2 cos ⁡ x - 1 ] d x + ∫ π 3 π [ 1 - 2 cos ⁡ x ] d x

Resolvendo...

A = 2 sin ⁡ x   - x 0 π 3 + x - 2 sin ⁡ x π 3 π

A = 2 sin ⁡ x   - x 0 π 3 + x - 2 sin ⁡ x π 3 π

Então, isso resultará em:

A = 2 sin ⁡ π 3   - π 3 - 2 sin ⁡ 0   - 0 + [ π - 2 sin ⁡ π - π 3 - 2 sin ⁡ π 3 ]

A = 3 - π 3 - 2 sin ⁡ 0   - 0 + [ π - 0 - π 3 - 3 ]

A = 3 - π 3 + [ π - π 3 + 3 ]

A = 2 3 + π 3

Prontinho!!

Resposta

A = 2 3 + π 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine as áreas das regiões compreendidas entre as retas e as curvas y = 7 - 2 x 2 E y = x 2 + 4
Determine as áreas das regiões compreendidas entre as retas e as curvas y = x 2 - 2 x E y = x
Determine as áreas das regiões compreendidas entre as retas e as curvas y = x 2 E y = - x 2 + 4 x
Desenhe a curva dada (coordenadas polares ). d )ρ = 2
Desenhe a curva dada (coordenadas polares ). b ) ρ cos ⁡ θ = 1 , - π 2θπ 2