Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.1 - Ex. 28
Esboce a região delimitada pelas curvas indicadas e encontre sua área.
Passo 1
Opa, bora resolver esse problema! O enunciado nos dá as curvas:
Para isso, devemos os pontos de interseções entre os gráficos para que assim a gente tenha os limites de integração para calcular a nossa área!!
Temos duas equações de grau positivas centradas em zero e uma reta que tem coeficiente angular negativo.
Assim, plotando, temos:
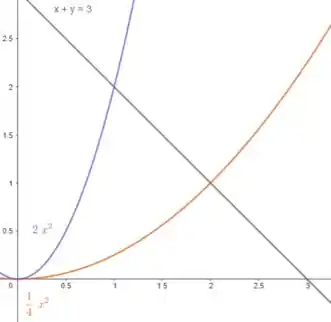
Passo 2
Agora, fazendo a interseção entre as funções, temos:
Isolamos o :
A gente bate o olho nessa equação e pensa “Hmm, fórmula de bhaskara”, mas o objetivo aqui é facilitar né não? Vamos reescrever a equação:
Logo, . Fazemos o mesmo para a outra função:
Organizando, temos:
Logo, .
Esse será o nosso intervalo de integração. Agora podemos calcular a área!!
Lembrando que a área que estamos calculando é a seguinte:
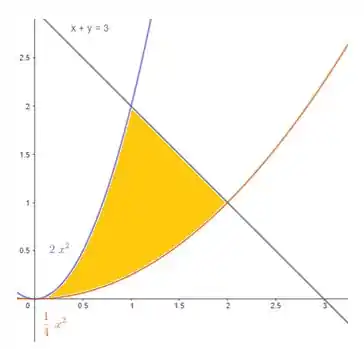
Passo 3
Organizando a integral, temos:
Resolvendo:
Então, isso resultará em:
Prontinho!! 😉