Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 7.8 - Ex. 41
Esboce a região e encontre sua área (se a área for finita).
Passo 1
A questão pede para fazermos um esboço da região e tentar sua área. A área que queremos calcular é a da região entre o eixo e a curva:
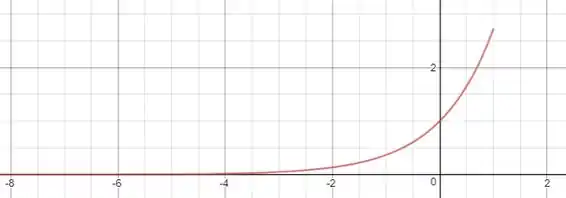
Essa área é representada por
Passo 2
Vamos tentar calcular a integral imprópria fazendo primeiro a integral
Passo 3
Agora vamos fazer o limite :
Portanto a área é finita e
Resposta
Exercícios de Livros Relacionados
Esboce a região e encontre sua área (se a área for finita). S = x , y x ≥ - 2 ,0 ≤ y ≤ e - x / 2 }
Esboce a região e encontre sua área (se a área for finita). S = x , y|0 ≤ y ≤ 2 x 2 + 9
Mostre que ∫ 0 ∞ e - x 2 d x = ∫ 0 1 - ln y d y interpretando as integrais como áreas.
Se g x = sen 2 x x 2 , use sua calculadora ou computador para fazer uma tabela de valores aproximados de ∫ 1 t g x d x para t = 2 , 5 , 10 , 100 , 1000 e 10000 . Parece que ∫ 1 ∞ g x d x é convergen