Esboce a região limitada pelas curvas dadas. Decida quando integrar em relação a x ou a y. Desenhe um retângulo típico de aproximação e coloque sua altura e largura. Entao calcule a área da região.

23.

Esboçando as curvas vamos ter que a área entre elas é essa:

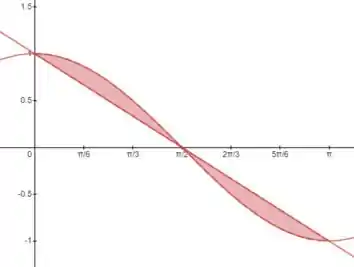
Podemos realizar as integrações em relação a para calcular a área desejada, então o retângulo vai ficar dessa forma:

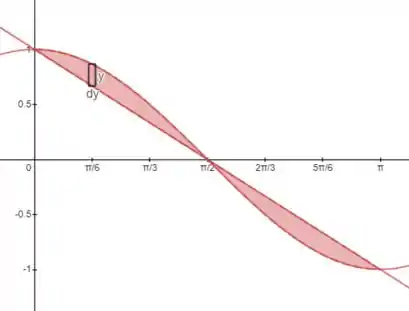
Aquele tamanho vai ser a diferença entre e , entre e , e a diferença entre e , entre e . Porém a área da parte positiva de y e da parte dnegativa de tem a mesma área, pela simetria do desenho, então, parar calcular a área total só precisamos integrar a área de até e multiplicar essa área por 2:

A integral de uma soma é igual a soma das integrais:

A integral do cosseno é o seno, e a interal de um polinômio é fácil de calcular, só aumentar um no expoente e dividir pelo expoente:

Aplicando os limites de integração: