Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.5 - Ex. 1n
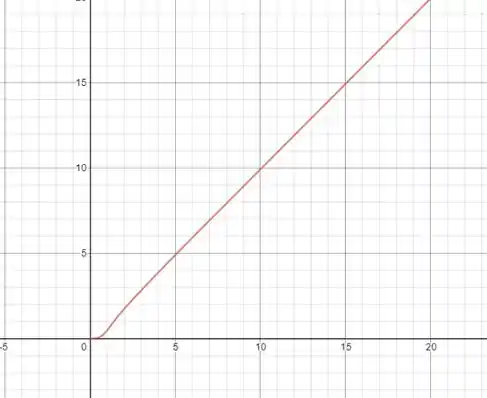
Desenhe a curva dada (coordenadas polares ).
Passo 1
Primeira coisa a se fazer é analizar os dados:
- ;
- O domínio é aberto em por que se substituirmos esse valor na equação ;
- Vamos escolher ângulos com metade dos valores dos Ângulos fundamentais para o cálculo com valores conhecidos, por causa do estar multiplicando 2.
Passo 2
A tabela vai ficar assim:
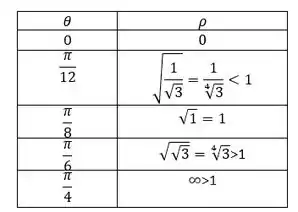
Então vemos que o raio é crescente e que perto de o raio tende a infinito(lembrando que não está definido no domínio, infinito não é uma resposta, é só uma noção pro desenho).
Passo 3
O desenho vai ficar assim:
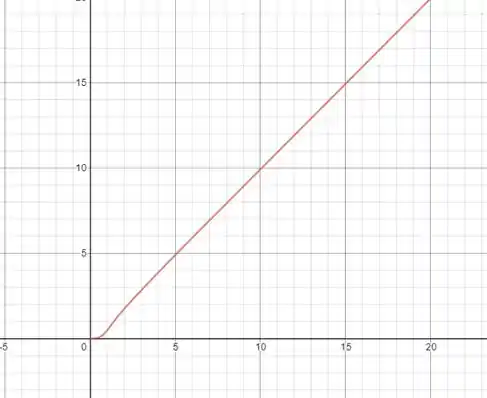
Perceba que o ângulo tende a e que o raio (nesse ângulo) tende a .
Resposta
Exercícios de Livros Relacionados
Determine a área entre a curva y = 2 1 - x e o intervalo - 1 ≤ x ≤ 1 do eixo x .
Determine a área das regiões compreendidas entre x = 3 s e n y c o sy e x = 0 ,0 ≤ y ≤ π 2
Determine a área da região entre a curva y = 3 - x 2 e a reta y = - 1 . Em relação a y
Determine a área das regiões compreendidas entre y = s e c π x 3 2 e y = x 1 3 , - 1 ≤ x ≤ 1
Determine a área entre a curva y = t g (x) e o eixo x de x = - (pi)/(4) até x = (pi)/(3) .