Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.5 - Ex. 1m
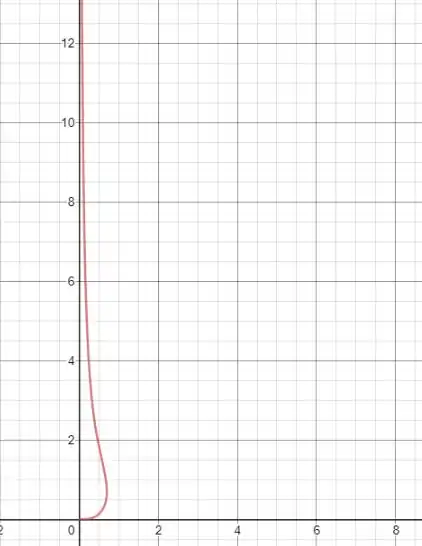
Desenhe a curva dada (coordenadas polares ).
Passo 1
Vemos que pela equação dada , e lembrar que , ou seja, conforme se aproxima de , se aproxima de .
Passo 2
Montando a tabela:
Então vemos que o raio é crescente e que perto de o raio tende a infinito(lembrando que não está definido no domínio, infinito não é uma resposta, é só uma noção pro desenho).
Passo 3
O gráfico vai ficar assim:
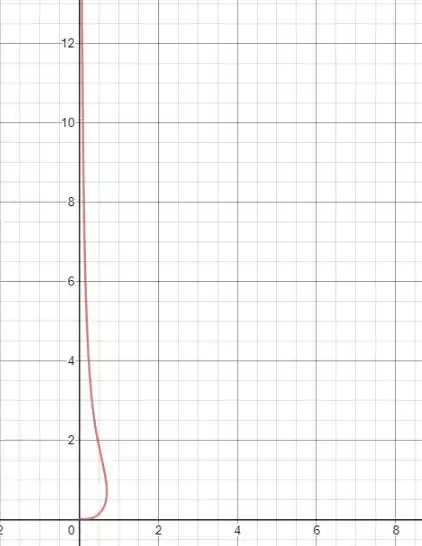
Resposta
Exercícios de Livros Relacionados
Nos Exercícios de 81 a 88, ache a área da região limitada pelas curvas e retas dadas. Faça uma figura mostrando a região e um elemento retangular da área. Expresse a medida da área como o limite de um
Determine a área das região no primeiro quadrante , delimitada pelas retas y = x e x = 2 A curva y = 1 x 2 e o eixo x
Determine a área das região em forma de hélice compreendida entre a curva x - y 3 = 0 e x - y = 0
Determine a área entre a curva y = 2 x 1 + x 2 e o intervalo - 2 ≤ x ≤ 2 do eixo x .
Determine a área da região” triangular” no primeiro quadrante , limitada à esquerda pelo eixo y e à direita pelas curva y = s e n ( x ) e y = c o s ( x )