Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 7

Esboce a região no plano que consiste em pontos cujas coordenadas polares satisfazem as condições dadas:

Passo 1

Eaee, beleza pura? Seguinte... a gente quer esboçar a região no plano em que as coordenadas polares obedecem a essa condição:

Para isso, vamos lembrar um pouquinho das coordenadas polares:

As coordenadas polares, representadas por e , descrevem a posição de um ponto no plano em relação a um ponto de referência (origem) e ao eixo , veja:

Em que é a distância do ponto à origem e é o ângulo formado entre o eixo positivo e uma linha que liga a origem ao ponto, medido no sentido anti-horário.

Agora vamos aplicar esse conceito na nossa inequação!!

Passo 2

Perceba que significa que queremos toda a área em que a distância do ponto à origem seja maior ou igual a .

De forma mais simples ainda, a nossa região é toooodo o plano, com exceção da circunferência de raio centrada na origem, veja:

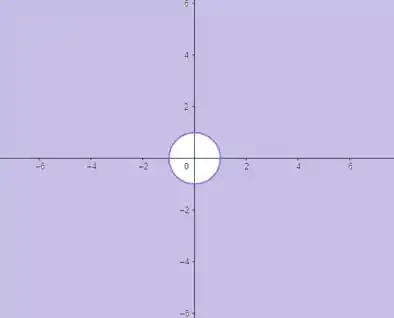
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercicos de 37 a 52, ache os pontos de intersecção dos gráficos do par de equações dadas. Faça um esboço de cada par de gráfico com o mesmo eixo polar e a mesma origem. r = 4 ( 1 + sen ⁡ θ ) r (

Nos exercicos de 37 a 52, ache os pontos de intersecção dos gráficos do par de equações dadas. Faça um esboço de cada par de gráfico com o mesmo eixo polar e a mesma origem. r = 2 cos ⁡ θ r = 2sen ⁡ θ

Nos exercicos de 37 a 52, ache os pontos de intersecção dos gráficos do par de equações dadas. Faça um esboço de cada par de gráfico com o mesmo eixo polar e a mesma origem. r = cos ⁡ θ - 1 r = cos ⁡

Nos exercicos de 37 a 52, ache os pontos de intersecção dos gráficos do par de equações dadas. Faça um esboço de cada par de gráfico com o mesmo eixo polar e a mesma origem. r = 3 r = 2( 1 + cos ⁡ θ )