Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.6 - Ex. 44
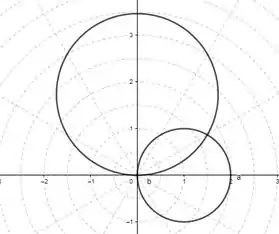
Nos exercicos de 37 a 52, ache os pontos de intersecção dos gráficos do par de equações dadas. Faça um esboço de cada par de gráfico com o mesmo eixo polar e a mesma origem.
Passo 1
O que o enunciado nos pede é para determinarmos os pontos de intersecção e depois fazer o esboço. Para determinar os pontos de intersecção basta igualar ou substituir um valor de r de uma equação na outra. A partir disso encontraremos o valor de dois ângulos que representarão os pontos que ele nos pede. Para elaborar o esboço, pode-se utilizar o programa de computador onde será mais fácil a visualização dos pontos de intersecção.
Passo 2
Fazendo as devidas substituição dos valores de r temos:
Assim, , dando os pontos
Passo 3
O esboço de cada par de gráfico com o mesmo eixo polar e a mesma origem é o seguinte:
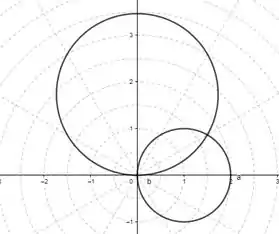
Resposta
Parte 1
Parte 2
