Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 13.1 - Ex. 11
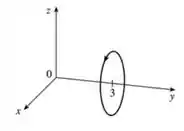
Esboce o gráfico da curva cuja equação vetorial é dada. Indique com setas a direção na qual o parâmetro cresce.
Passo 1
Fala galera. Tudo belezinha?
Vamos começar a resolver a questão!
Primeiro de tudo iremos analisar o enunciado e separar os dados importante eles nos ajudarão a encontrar o nosso objetivo, que é o Queremos esboçar o gráfico da seguinte função paramétrica, mostrando a direção em que o parâmetro cresce:
Pois então, mão na massa!
Passo 2
A direção na qual o parâmetro cresce ao longo da curva definida por , podemos usar o conceito de derivadas e vetor tangente à curva.
Vou te mostrar como se faz!
Primeiro, calcule a derivada da função vetorial em relação a . A derivada nos dará o vetor tangente à curva em cada ponto.
Portanto,
Passo 3
A partir da análise do vetor tangente , observamos que o componente 𝑥 (representado por ) é sempre positivo ao longo da curva para no intervalo .
Portanto, a direção na qual o parâmetro cresce ao longo da curva é na direção positiva do eixo , ou seja, da esquerda para a direita quando olhamos na direção do eixo .
Passo 4
Para observar a direção em que o parâmetro cresce, vamos aplicar alguns valores em :
Em
Em
Ou seja, o gráfico vai ao sentido da direção
Passo 5
Como no eixo temos uma constante igual a , isso quer dizer que o gráfico é deslocado no sentido do eixo em .
Assim, a forma do gráfico é:
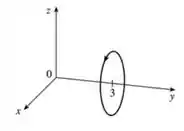
Resposta
