Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 13.1 - Ex. 10
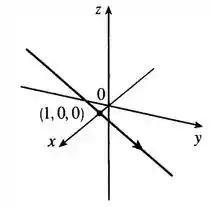
Esboce o gráfico da curva cuja equação vetorial é dada. Indique com setas a direção na qual o parâmetro cresce.
Passo 1
Fala galerinha. De boa por ai?
A questão pede para esboçar o gráfico da curva definida pela equação vetorial e indicar a direção na qual o parâmetro cresce ao longo dessa curva.
Para resolver esta questão precisamos
- Interpretar a equação vetorial
- Parametrizar as coordenadas
- Esboçar o gráfico e indicar a direção do parâmetro .
Vamos começar agora!
Passo 2
Queremos esboçar o gráfico da seguinte função paramétrica, mostrando a direção em que o parâmetro cresce:
Passo 3
Se , podemos identificar as componentes.
Logo
Aplicando a equação em e :
Vamos analisar!!!
Passo 4
Todas as variáveis no problema aparecem de forma linear, o que significa que será uma reta a curva que queremos esboçar.
Além disso, quanto maior o valor de , maior o valor de . Assim, o parâmetro cresce na direção de crescimento de .
Além disso, ela respeitará que as equações lineares: e .
Passo 5
De acordo com os cálculos feitos, temos que
- Plano (para ): É uma linha reta inclinada com inclinação positiva no plano .
- Plano (para): É uma linha reta inclinada com inclinação positiva no plano .
- Plano (para ): É uma linha reta inclinada com inclinação negativa no plano .
Chagou a hora de confirmarmos com a construção do gráfico!
Assim, o gráfico da equação é:
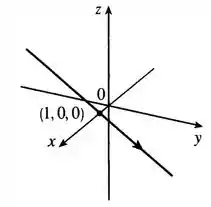
Resposta
