Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.4 - Ex. 13
Escreva graficamente a curva e encontre a área que ela encerra.
Passo 1
Falaee, tudo tranquilinho??
Bom... o enunciado nos deu a seguinte expressão dada em coordenadas polares):
Queremos calcular área total dessa curva.
Em outras palavras, queremos calcular a área delimitada sob essa curva:
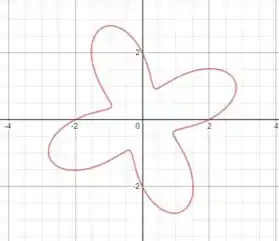
Para isso, a área é dada pela seguinte integral:
Agora bora aplicar!! 😉
Passo 2
Como a curva está nos quatro quadrantes, o intervalo do ângulo será , onde os extremos serão os limites da integral da área:
Ficando com:
Passo 3
Vamos primeiro resolver a integral indefinida e substituir os limites ao final:
Abrindo o polinômio:
Pela linearidade da integral:
Usando a identidade trigonométrica:
Teremos:
Integrando cada termo:
Tirando MMC:
Passo 4
E por último, substituindo os limites, temos:
Simplificando, obtemos: