Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.4 - Ex. 24
Encontre a área da região que está dentro da primeira curva e fora da segunda curva.
24. ,
Passo 1
Olá, meu brother. Vamos aprender um pouco mais hoje.
Temos em mãos duas regiões:
E queremos encontrar a área dentro da primeira curva e fora da segunda curva.
A curva que é a interior é a curva:
E a exterior:
A região que estamos procurando a área será:
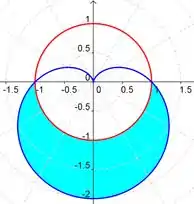
Veja que temos algumas coisas a se pensar antes de começarmos os cálculos. O primeiro é quem são os limites de integração. Você já deve ter pensado em como encontrá-los, precisamos igualar as equações das duas curvas.
E veja que a área da região que queremos é dada pelo cálculo da área da figura com delimitação azul, menos a área da figura com delimitação em vermelho, tudo isso dentro dos nossos limites de integração.
Pela equação da área entre duas regiões, teremos:
Passo 2
Primeiro passo então, vamos calcular os limites de integração:
Pela equação da área entre duas regiões, teremos:
Onde e . Substituindo tudo:
Passo 3
Vamos primeiro resolver a integral indefinida para no final colocarmos os limites:
Abrindo o polinômio:
Usando a propriedade trigonométrica:
Ficamos com:
Pela linearidade:
Integrando cada termo:
Passo 4
Substituindo os limites de integração, lembrando que o nosso limite de integração é :
Acabou-se o que era doce.