Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.4 - Ex. 34d
Espirais As coordenadas polares são perfeitas para definir espirais. Desenhe as espirais a seguir.
- Uma espiral hiperbólica:
Passo 1
Fala gente tudo bem? Vamos plotar nossa espiral a partir da equação dada, mas como faremos isso? Bom, primeiro precisamos achar os nossos pontos, nesse exercício consideremos o intervalo de 0 a .
Como r é , nossos pontos ficam:
Passo 2
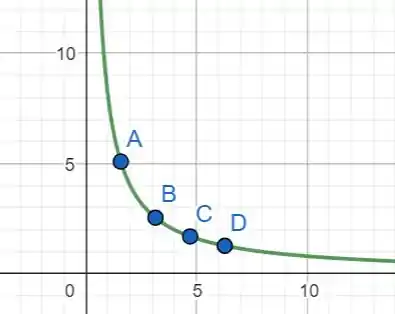Com os pontos, agora vamos montar nosso gráfico utilizando o Geogebra:
Como vimos, esse gráfico precisa se tornar uma espiral, dessa maneira devemos angular os nossos pontos e girar nossa reta.
E assim, usando o Wolfram para adequar nosso gráfico corretamente, o resultado fica:
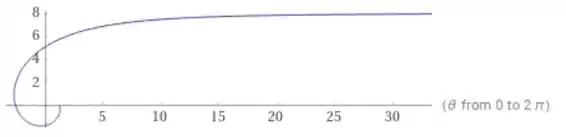
Bora continuar!!!
Resposta
Exercícios de Livros Relacionados
Encontrar um par de coordenadas polares do seguinte ponto: 1,1
Encontrar as coordenadas cartesianas do seguinte ponto dado em coordenadas polares. 4 , 5 π 8
Assinalar o ponto dado em coordenadas polares e depois escrever as coordenadas polares para o mesmo ponto, tal que: r tenha sinal contrário θ tenha sinal contrário 4 , 5 π 6
Encontrar um par de coordenadas polares do seguinte ponto: - 1 , - 1
Encontrar as coordenadas cartesianas do seguinte ponto dado em coordenadas polares. 3 , 13 π 4