Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.6 - Ex. 45
Estime o valor de
traçando o gráfico da função
Faça uma tabela de valores de para estimar qual será o valor do limite
Demonstre que sua conjectura está correta
Passo 1
Opa! Vamos fazer essa questão?! O enunciado nos deu ao limite:
E nos pediu três coisas: A primeira é estimar o valor do limite a partir do esboço do gráfico de sua função. Pra isso a gente vai plotar o gráfico e olhar pra onde vai a função quando temos valores de negativos muito grandes!
A segunda é fazer uma tabelinha com valores de e , isso pode ser a primeira coisa a fazer! Daí a gente já usa esses valores pra montra o gráfico da letra (a)!
Na tabelinha é importante a gente pegar valores negativos pequenos e ir aumentando muuuuito. Estamos indo pra menos inifinito!
Passo 2
Vamos começar com a letra então, montando a tabelinha! Temos que:
Olhando a tabela a gente vê que quando pegamos valores negativos muito grandes, tendendo a infinito o tende a .
Passo 3
Agora vamos pegar os valores acima e montar o gráfico:
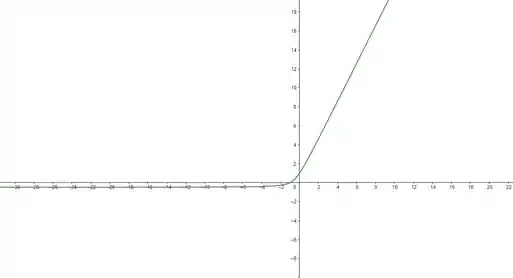
Como a gente consegue ver, a nossa função quando vai para , fica parecendo uma reta horizontal, vamos dar um zoom pra ver quem é essa reta!
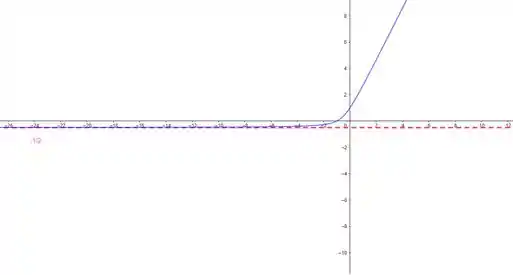
Aqui a gente consegue ver que quando temos que .
Passo 4
Para ver se o limite estimado esta correto vamos calcular esse limite
Vamos multiplicar em cima e embaixo pelo conjugado:
Isso nos dá:
Ajeitando isso dai ficamos com:
Vamos colocar em evidencia dentro da raiz ficando com:
Dividindo todo mundo por :
Calculamos o limite:
Que é a mesma coisa que
Então estimamos corretamente!