Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.1 - Ex. 53
Dois carros, e , largam lado a lado e aceleram a partir do repouso. A figura mostra os gráficos de suas funções velocidade.
Qual carro estará na frente após minuto? Explique.
Qual o significado da área da região sombreada?
Qual carro estará na frente após minutos? Explique.
Estime quando os carros estarão novamente lado a lado.
Passo 1
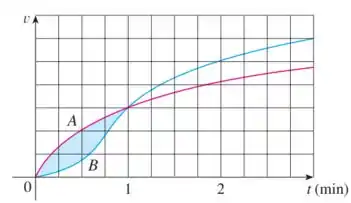
Opa! Aqui temos dois carros, e que partiram do mesmo ponto em um mesmo instante. Se liga nesse gráfico que nos dá a velocidade em função do tempo:
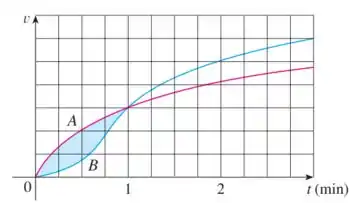
A primeira coisa que devemos responder é qual carro estará na frente após minuto!
Bem, se a gente integrar cada curva teremos:
A velocidade é nada mais nada menos que a derivada da distância em função do tempo. Certo?!
Isso quer dizer que a integral da velocidade é a distância! Então a curva com a maior área sobre ela percorreu a maior distância. Concorda?!
Então podemos dizer que após o primeiro minuto o carro esta na frente!
Se eu fizer:
Passo 2
Agora a letra b)!
Se eu fizer:
Então teremos a distância entre os dois carros.
Essa integral representa a área sombreada da imagem, que é a distância entre e após um minuto!
Passo 3
Para a letra c) temos que após 2 minutos, o carro ainda está na frente.
Isso acontece porque apesar do carro ter aumentado sua velocidade, a área abaixo da curva de ainda é maior que a área abaixo da curva de .
Por fim, na letra d) os carros estarão juntos novamente quando a área de for a mesma área de , que ocorre no gráfico aproximadamente em
Prontinho!
Resposta
Após um minuto, o carro está na frente.
A distância entre e após um minuto.
Após 2 minutos, o carro ainda estará na frente,.
Os carros estarão juntos novamente em