Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 8.3 - Ex. 14
Uma barragem vertical tem um portão semicircular, como mostrado na figura. Calcule a força hidrostática contra o portão.
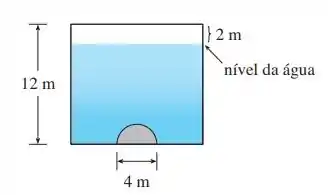
Passo 1
Olá, meu amigo, Yuri aqui e estarei te ajudando a resolver essa atividade.
Aqui iremos calcular a pressão hidrostática no portão, O que iremos calcular então é a soma resultante de micro pressões em microáreas do nosso portão. Isso te lembra algo? Sim, iremos utilizar a integral para encontrarmos a pressão.
O esboço do portão é o seguinte:
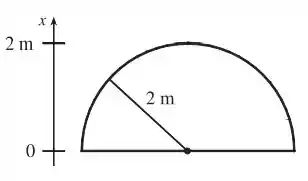
Passo 2
Assim, nossa força é
Passo 3
Agora utilizaremos substituição por partes da seguinte forma:
Então,
Resposta
.
Exercícios de Livros Relacionados
41- Placa inclinada Calcule a força do fluido em um lado de uma placa quadrada de 5 por 5 pés se a placa estiver no fundo de uma piscina cheia de água a uma profundidade de 8 pés eDeitada com seu lado
43- O tanque de metal cúbico mostrado aqui tem uma portinhola parabólica que é mantida no lugar por meio de parafusos, e que foi projetado para suportar uma força de fluido de 160 lb sem se romper. O
44- As placas nas extremidades do cocho mostrado aqui foram projetadas para suportar uma força de fluido de 6667 libras. Quantos pés cúbicos de água o tanque pode conter sem ultrapassar essa limitação
45- Uma placa retangular vertical com a unidades de comprimento por b unidades de largura é submersa em um fluido de peso específico w com suas bordas mais longas paralelas à superfície do fluido. Det
46- ( Continuação do Exercício 45.) Mostre que a força exercida pelo fluido em um lado da placa é o valor médio da pressão ( determinada no Exercício 45) vezes a área da placa.