Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.2 - Ex. 78
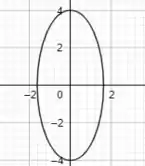
O exercício a seguir apresenta uma equação de elipse. Coloque a equação no formato padrão e esboce a elipse.
Passo 1
De início já notamos que a equação não está no formato padrão da equação de elipse. O formato padrão é o seguinte:
Assim como discutido na seção 1.2 do George, o gráfico dessa equação para apresenta eixo principal horizontal. Caso contrário, se , o gráfico dessa equação apresenta eixo principal vertical. Em ambos os casos, o eixo principal tem o maior comprimento.
Passo 2
Como o lado direito da equação tem que dar 1, então para escrevermos a equação que nos foi dada no formato padrão da equação de elipse, devemos dividir todos os membros por 112, beleza? Fazendo essa divisão, teremos:
Simplificando as constantes, teremos o seguinte:
e
Passo 3
Agora que já temos os valores de e e a função no formato padrão, basta plotarmos o gráfico da elipse! Nesse caso, como , então o eixo principal será vertical. Dessa forma, o gráfico da elipse será:
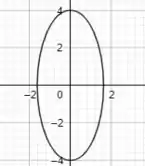
Resposta
