Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.5 - Ex. 13
Nos exercícios de 13 a 20, coloque num gráfico o ponto com coordenadas polares dadas; dê, então, dois outros conjuntos de coordenadas polares para o mesmo ponto; um com o mesmo valor de r e outro com o sinal oposto a r.
13.
Passo 1
Bom, o enunciado nos pede o valor do próprio ponto com um conjunto de coordenadas diferentes, primeiro faremos o gráfico do ponto:
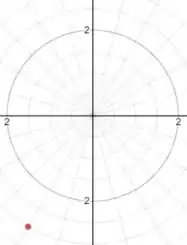
Passo 2
Para as coordenadas com o mesmo sinal de r, podemos fazer a rotação por valores positivos ao invés de negativos, então precisaremos rotacionar em para obtermos o mesmo ponto. Ficaremos então com as coordenadas:
Passo 3
E para coordenadas com sinal oposto ao de r, precisaremos somar ao valor da coordenada dada no enunciado:
E as coordenadas serão:
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Nos exercícios 23 e 24, ache um conjunto de coordenadas polares dos pontos cujas coordenadas cartesianas retangulares são dadas. Tome r0 e 0 ≤ θ ≤ 2 π .24(a) ( 3 ,- 3 )
Nos exercícios de 5 a 10, marque num gráfico o ponto com as coordenadas polares dadas; ache então outro conjunto de coordenadas polares para o mesmo ponto para o qual a r0e0 ≤ θ ≤ 2 π ; br0e - 2 πθ ≤
Nos exercícios de 1 a 4, marque o ponto com o conjunto de coordenadas polares dadas.4. a5 , - 2 π 3 ; b2 , - 7 π 6 ; c- 5 , 2 π 3 ; d- 2 , 7 π 6 ; e- 4 , - 5 π 4
Nos exercícios de 5 a 10, marque num gráfico o ponto com as coordenadas polares dadas; ache então outro conjunto de coordenadas polares para o mesmo ponto para o qual a r0e0 ≤ θ ≤ 2 π ; br0e - 2 πθ ≤
Nos exercícios de 5 a 10, marque num gráfico o ponto com as coordenadas polares dadas; ache então outro conjunto de coordenadas polares para o mesmo ponto para o qual a r0e0 ≤ θ ≤ 2 π ; br0e - 2 πθ ≤