Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.1 - Ex. 1
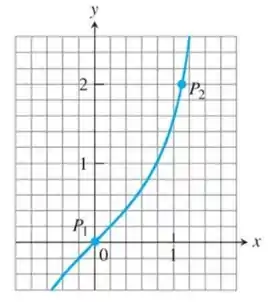
Nos Exercícios 1-4, use a grade e uma régua para fazer uma estimativa aproximada do coeficiente angular da curva (em unidades de y por unidade de x) nos pontos e .
Passo 1
Nesse exercício ele pede para acharmos o coeficiente angular da curva em P1 e P2. Pra encontrar isso, vamos precisar traçar duas retas tangentes uma no ponto P1 e outra no ponto P2 e calcular o coeficiente!
Passo 2
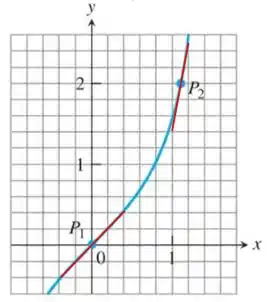
Depois de traçar as tangentes, já podemos estimar os coeficientes angulares, que nada mais é do que a inclinação da reta. Para estimar a gente precisa pegar dois pontos que passem pelas tangentes e calcular o .
Obs.: Tudo bem se os pontos que você escolher não forem os mesmos que os meus, mas o resultado tem que dar parecido!
Passo 3
Para P1, os pontos escolhidos foram (0,2;0,2) e (-0,2;-0,2):
Para P2, os pontos escolhidos foram (1,2;2,4) e (1,0;1,4):
Prontinho, encontramos os coeficientes angulares.