Exercícios de Propriedades de Derivadas - Lista de Exercícios Resolvida
Questão 6
Sendo a função dada pelo gráfico abaixo, diga onde a derivada de é positiva, negativa ou nula.
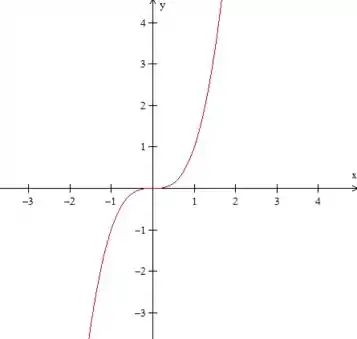
Questão 8
Considere . Sejam e pontos no domínio tais que as retas tangentes ao gráfico da nestes pontos sejam paralelas. Mostre que o valor da soma independe da escolha dos pontos e calcule este valor.
Ver solução completaQuestão 9
Considere a função definida pelo gráfico abaixo,
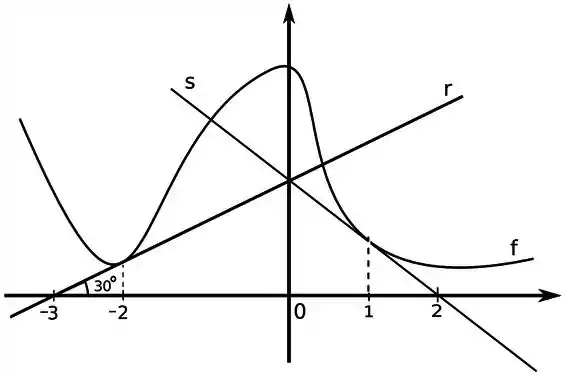
Sabendo que a reta é tangente ao gráfico da em e a reta tangente ao gráfico da em
- Determine a equação da reta
- Determine e
- Determine a equação da reta
- Determine e
Questão 10
Considere a função definida pelo gráfico abaixo, a reta tangente ao gráfico da em e a reta tangente ao gráfico de em .
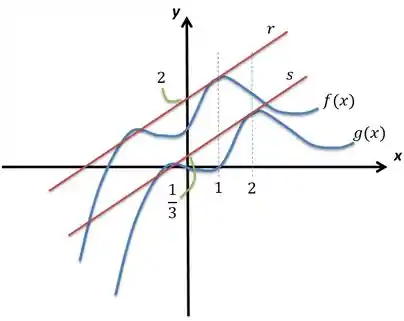
Determine:
A equação das retas e
Ver solução completa
Questão 11
A equação de movimento de um objeto é dada por e em metros e em segundos.
- Determine a velocidade em m/s
- Determine a aceleração em m²/s
- Determine a aceleração no
- Determine a aceleração no(s) instante(s) em que a velocidade é igual a 0
Questão 12
Calcule a derivada das seguintes funções, usando as regras de derivação:
Ver solução completaQuestão 18
Considere as afirmações a seguir
Seja uma função diferencial em tal que e . Então existe tal que ;
Seja uma função diferencial em e suponha que existe tal que . Então ;
Sejam e funções diferenciáveis em tais que para todo e suponha, além disso, que . Então .
Podemos concluir com certeza que:
: Apenas a afirmação é verdadeira.
: Apenas as afirmações e são verdadeiras.
: Todas as afirmações são verdadeiras.
: Apenas as afirmações e são verdadeiras.
: Apenas as afirmações e são verdadeiras.
Ver solução completaQuestão 29
2. Determine o que se pede.
- Se uma função possui derivada , calcule e .
Questão 37
Considere e funções definidas pelos gráficos abaixo. Sabendo que é tangente ao gráfico da e ao da em , e que corta os eixos nos pontos indicados, faça um esboço, no mesmo par de eixos, do gráfico das derivadas e .
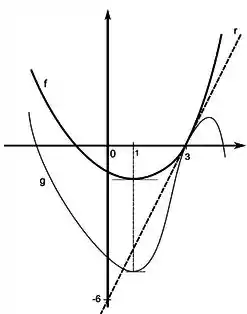
Questão 38
Sejam uma função quadrática e a reta tangente ao gráfico de no ponto . Sabendo que e se intersectam o eixo nos pontos e respectivamente, determine
Ver solução completaQuestão 39
Neste exercício vamos mostrar que se , então
- Mostre que
- Mostre que
Sugestão: utilize que
Questão 40
Nas videoaulas, você viu as primeiras regras de derivação (veja quadros abaixo com três possíveis escritas). Sejam u e v funções de x e c um número real.
Utilize essa tabela e a tabela da lista de exercícios 2.5 na resolução dos exercícios.
Determine a derivada das funções abaixo.
Ver solução completaQuestão 42
Considere a função exponencial , em que e .
- Mostre que
- Mostre que
- O que acontece com a derivada quando , isto é, quando a função é ?
Questão 43
Dois carros iniciam o movimento partindo de um mesmo ponto. Um viaja para o sul a e o outro para oeste a . A que taxa está crescendo a distância entre os carros duas horas depois?
Um carro A está se movimentando para o oeste a 90km/h e o carro B está se movimentando para o norte a 100 km/h. Ambos vão em direção à interseção de duas estradas. A que taxas os carros se aproximam um do outro quando o carro A está a 60 m e o carro B está a 80 m da interseção?
Ver solução completaQuestão 44
Nos exercícios 18 a 21, use o gráfico da função para determinar os valores de em que a função é diferenciável e indique os valores de em que a derivada (i) nula (ii) positiva (iii) negativa.
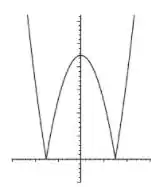
Questão 45
Use o gráfico da função para determinar os valores de em que a função é diferenciável e indique os valores de em que a derivada é nula, positiva e negativa.
Ver solução completaQuestão 46
Nos exercícios 18 a 21, use o gráfico da função para determinar os valores de em que a função é diferenciável e indique os valores de em que a derivada (i) nula (ii) positiva (iii) negativa.
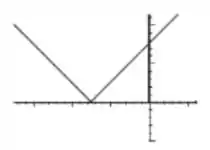
Questão 47
Nas videoaulas, você viu as primeiras regras de derivação (veja quadros abaixo com três possíveis escritas). Sejam u e v funções de x e c um número real.
Utilize essa tabela e a tabela da lista de exercícios 2.5 na resolução dos exercícios.
Determine a derivada das funções abaixo.
Ver solução completaQuestão 49
O movimento retilíneo uniforme (MRU) é caracterizado por um movimento que não possui aceleração, em outras palavras, . Fixando as condições inicias como sendo e , essa situação é matematicamente resumida por: determine a função que satisfaz
- Mostre que, para quaisquer números A e B, a função satisfaz
- Mostre que, para satisfazer e , então
- Determine para a função obtida no item anterior para confirmar que, em um movimento em que a aceleração é igual a 0, a velocidade é constante.
Questão 51
Seja um número real fixado e considere a função . a tabela nos diz que . Nesse exercício vamos deduzir esta fórmula apenas no caso em que é um número natural positivo.
- Verifique que os produtos abaixo são verdadeiros
- Verifique que na expressão há parcelas na soma
- Considere e, usando o item (a), mostre que
- Mostre que
Sempre que for diferente de
Passo 1
Oi pessoal, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui! Bora lá?
No primeiro item ela pede para mostrarmos uma série de produtos, então precisamos, um a um, ir calculando e vendo a equivalência, beleza?

No segundo item o problema pede para verificar que há parcelas: aqui também precisamos analisar a expressão e ver a equivalência

E nos dois últimos itens? Vamos usar os resultados de (a) e (b) e aí mostrar a primeira das fórmulas de derivada que conhecemos

Calma! A questão é um pouco longa e complicada, mas estou aqui!
Vamos fazer passo a passo, juntinhos!
Passo 2
Letra (a): nesse primeiro item vamos mostrar os seguintes produtos
O primeiro e o segundo são bem conhecidos (basta aplicar a propriedade distributiva):
Beleza? Agora vamos mostrar o terceiro:
É só cortar os termos semelhantes! Esse também é conhecido como diferença entre cubos

Tranquilo?
Agora o quarto produto:
E novamente simplificando temos
Você percebeu um padrão?

 Os termos ‘mistos’ vão sempre se cancelando! Ficamos apenas com os extremos (com 1 unidade a mais no expoente)!
Os termos ‘mistos’ vão sempre se cancelando! Ficamos apenas com os extremos (com 1 unidade a mais no expoente)!
Aí então vem a nossa generalização! Se tivermos um produto assim
O resultado vai ficar apenas com os termos extremos, com uma unidade a mais no expoente
Beleza? Primeiro ponto concluído com sucesso!
Ver solução completaQuestão 52
Neste exercício vamos mostrar que se , então
- Mostre que
- Mostre que
Sugestão: utilize que
Questão 53
Suponha que e sejam, ambas, funções diferenciáveis satisfazendo para todo . Então podemos afirmar que os gráficos de e :
- Não possuem mais do que uma interseção.
- Possuem exatamente uma interseção.
- Podem possuir mais de uma interseção.
- Não possuem interseção.
- Têm uma reta tangente em comum no ponto de interseção.
Questão 55
6) Um balão sobe verticalmente acima de uma estrada plana a uma velocidade constante de . Quanto está a acima do solo, uma bicicleta que se desloca a uma velocidade constante de passa sobre ele. A que taxa a distância entre a bicicleta e o balão aumentará 3 segundos mais tarde?
Ver solução completaQuestão 56
Encontre a derivada das seguintes funções nos pontos dados
Para , encontre .
Ver solução completaQuestão 57
Nas videoaulas, você viu as primeiras regras de derivação (veja quadros abaixo com três possíveis escritas). Sejam u e v funções de x e c um número real.
Utilize essa tabela e a tabela da lista de exercícios 2.5 na resolução dos exercícios.
Determine a derivada das funções abaixo.
Ver solução completaQuestão 58
Considere um movimento em que a aceleração é dada por e atribua as condições inicia e .
- Mostre que essa situação pode ser descrita por encontrar uma função que satisfaz
- Mostre que, para quaisquer números e , a função satisfaz
- Mostre que para satisfazer e , então
Questão 60
Determine A, B, C para que a função seja solução da equação diferencial
Ver solução completaQuestão 61
11) No instante horas um veículo está quilômetros à leste de um ponto de referência na estrada.
(a) Qual a velocidade no instante ? Nesse instante, o veículo está se afastando ou se aproximando do ponto de referência?
(b) Onde está o veículo quanto a velocidade é zero?
Ver solução completaQuestão 62
Supondo que a posição de uma partícula é dada por , resolva os itens a seguir
a) Calcule a velocidade média da partícula entre os instantes e
b) Calcule a velocidade instantânea da partícula quando
Ver solução completaQuestão 63
Calcule a taxa de variação do volume de um balão esférico em relação ao seu raio, quando o raio do balão é igual a
Ver solução completaQuestão 64
A Lei de Gravitação de Newton diz que a intensidade da força exercida por um corpo e massa sobre um corpo de massa é
Em que é a constante gravitacional e é a distância entre os corpos. Calcule e explique seu significado. O que o sinal de menos indica?
Ver solução completaQuestão 65
A posição de uma partícula sobre uma linha reta graduada em metros no instante segundos é dada por
- Determine
- Determine
- Em quais instantes a partícula está em repouso?
- Quando a partícula está se movendo para frente? E quando está se movendo para trás?
- Qual é o deslocamento da partícula entre os instantes e ?
- Qual é a distância percorrida pela partícula entre os instantes 0 e 5s?
- Para que valores de tem-se Para quais valores de tem-se Para quais valores de tem-se
- Quando a partícula está acelerando ou freando?
Questão 70
Considere a função logarítmica , em que e .
- Mostre que
- Mostre que para temos , em que e
- Mostre que
- O que acontece com a derivada quando , isto é, quando a função é ?
Questão 71
Suponha que, após ser lançado para cima, a posição de um projétil é dada por , até o instante em que ele retorna ao solo
a) Calcule o tempo necessário para que o projétil retorne ao solo
b) Determina a velocidade do projétil, para . O que acontece com a velocidade para ?
c) Determine a altura máxima atingida pelo projétil e o tempo necessário para que ele atinja esta altura. O que ocorre com a velocidade nesse instante?
Ver solução completaQuestão 72
Quantas retas tangentes ao gráfico de f(x) = são paralelas à reta ? Determine a equação dessas retas tangentes.
Ver solução completaQuestão 73
Um cabo pendurado entre dois postes toma a forma de uma curva que é o gráfico de uma função que satisfaz a equação diferencial
em que é a densidade linear (massa por unidade de comprimento) do cabo, é a aceleração da gravidade e é a tensão do cabo no ponto mais baixo. Mostre que a função é uma solução da equação diferencial acima.
Ver solução completaQuestão 74
Suponha que a relação entre o comprimento L, em metros, e o peso P, em kg, de um determinado peixe seja dada por Suponha ainda que a taxa de variação do comprimento e, relação ao tempo, dado em anos, satisfaz a equação:
- Determine o comprimento do peixe de no caso em que
- Determine a taxa de variação do peso em relação ao tempo
- Use os itens anteriores para determinar a taxa de variação do peso do peixe, em relação ao tempo, para um peixe de 20 kg
Questão 75
Questão 1.2 - A equação
(a) tem exatamente uma raiz real negativa, mas não tem uma raiz real positiva.
(b) tem pelo menos três raízes reais.
(c) tem exatamente uma raiz real positiva, mas não tem uma raiz real negativa.
(d) não tem raízes reais.
Ver solução completaQuestão 83
Utilizando as regras de derivação, calcule a derivada das seguintes funções:
a)
Ver solução completaQuestão 84
Utilizando as regras de derivação, calcule a derivada das seguintes funções:
f)
Ver solução completaQuestão 93
5. Considere duas funções, e , deriváveis em 3 tais que
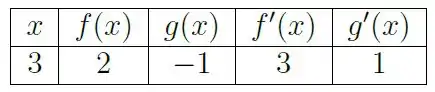
O valor de é:
a) -2
b) -1
c) 1
d) 2
e) 3
Ver solução completaQuestão 97
2. Determine o que se pede.
- Se uma função possui derivada , calcule , e .
Questão 99
Seja um polinômio de grau 3, com três raízes reais distintas. Mostre que tem um ponto de inflexão, que é a média aritmética das três raízes.
Ver solução completaQuestão 100
Seja um número real fixado e considere a função constante . Aplique a definição de limite e verifique que .
Ver solução completaQuestão 102
Utilizando as regras de derivação, calcule a derivada das seguintes funções:
b)
Ver solução completaQuestão 109
Considere a função definida pelo gráfico abaixo.
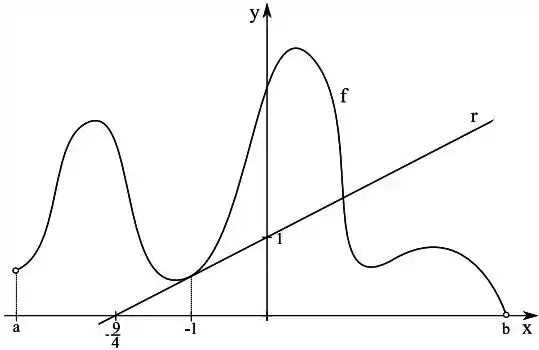
- Indique os pontos onde é zero. (Justifique graficamente, desenhando a reta tangente)
- Indique os intervalos onde é positiva. Indique os intervalos onde é negativa. (Justifique graficamente)
- Faça um esboço do gráfico da
- Sabendo que a reta é tangente ao gráfico da em , calcule e