Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.5 - Ex. 21
Nos Exercícios de 17 a 24, ache o ponto de inflexão do gráfico da função dada, se existir. Determine onde o gráfico é côncavo para cima e onde ele é côncavo para baixo. Faça um esboço do gráfico.
Passo 1
Para começar precisamos determinar os pontos de inflexão do gráfico, ou seja, o ponto onde a função muda a direção da concavidade. Para descobrir estes pontos o primeiro passo é descobrir a derivada segunda da nossa função:
Uma vez descoberta a derivada segunda, os pontos de inflexão são caracterizados por .
Passo 2
Segundo a Definição 4.5.4, determinado ponto c é de inflexão se passar por ele uma reta tangente e se a concavidade mudar de direção em valores maiores e menores que o ponto c.
A derivada primeira da função indica a inclinação da reta tangente àquele ponto. Sabendo que:
Lembrando que, para o limite bilateral existir os limites laterais direito e esquerdo devem ser iguais.
Então:
Ou seja, há uma reta tangente que passa sobre o ponto .
Analogamente:
Analisando a mudança de direção da concavidade:
Sendo assim, há reta tangente que passa por esse ponto e há mudança na concavidade, então é um ponto de inflexão.
Desenhando o gráfico da função:
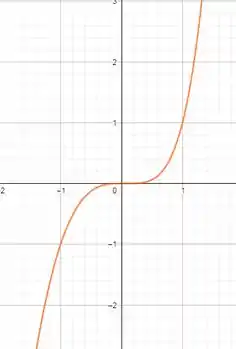
Resposta
Ponto de inflexão: .