Desenhe um esboço do gráfico da equação Sugestão: o gráfico não é aquele de uma função. Entretanto, a parte no primeiro quadrante é o gráfico de uma função. Obtenha essa porção e então complete o gráfico por simetria. A concavidade desempenha um papel importante.).
Passo 1
Para começar podemos isolar y, quando :
Sendo assim, está definido para Diferenciando com relação a x:
Então, é negativo e, consequentemente, o gráfico decresce no intervalo de Analisando,
Sendo assim, quando x se aproxima de 0 o gráfico possui uma reta vertical no ponto (0,1). Por simetria, o gráfico apresenta uma reta tangente horizontal no ponto (1,0).
O próximo passo é obter a derivada segunda:
Reorganizando:
Sendo assim, no intervalo ou seja, a concavidade é voltada para cima no primeiro quadrante.
Agora, precisamos desenhar o gráfico da função. Como dito no enunciado, a parte do primeiro quadrante é o gráfico da função, e nós já descobrimos que a concavidade é voltada para cima e a função é decrescente. Sabendo que o gráfico é simétrico aos eixos x e y, temos:
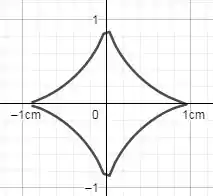
Resposta
Ei, a resposta está no passo a passo :)