Nos Exercícios de 33 a 40, ache uma equação da parábola com as propriedades dadas. Faça um esboço do gráfico.
40. Os extremos do latus rectum são e .
Passo 1
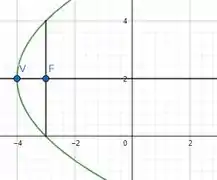
Para resolver esse problema, precisamos entender o que é o latus rectum. Ele é um seguimento de reta que tem o foco como ponto médio, e ele vai de uma extremidade a outra da parábola, como a figura mostra a seguir:
Passo 2
Sabemos que o valor absoluto do latus rectum tem como valor igual a , usando o que o enunciado nos deu o comprimento dele é:
Como o foco é ponto médio desse segmento, temos que:
Passo 3
Agora observando as disposições dos pontos extremos do latus rectum e do foco, constatamos que a parábola tem concavidade para cima.
Então temos o seguinte modelo de equação da parábola:
Agora precisamos achar os valores de h, p e k para a situação que temos.
Passo 4
O valor de p já achamos no passo 2, agora vamos achar h e k.
Achar h e k é fácil, eles representam as coordenadas do vértice, onde h é a coordenada x do vértice e k a coordenada y. E para achar o vértice basta lembrar que ele deve ficar na mesma reta do foco e na direção da abertura da parábola, a uma distância do foco.
Assim:
As coordenadas do vértice são:
Passo 5
Agora colocando tudo que encontramos na equação ela toma a seguinte forma:
Passo 6
O gráfico que representa a equação da parábola é da seguinte maneira:
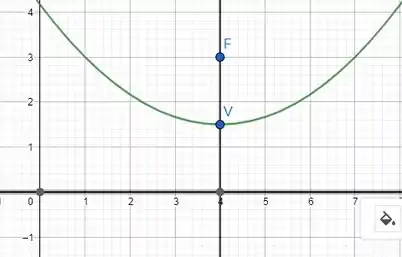
Resposta
Ei, a resposta está no passo a passo :)