Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.9 - Ex. 24
Nos exercícios de 21 a 28, ache e para a curva dada no ponto cujo valor de é o indicado. Faça um esboço da curva e mostre e .
24.;
Passo 1
O enunciado nos pede para achar o ângulo que é dado pela equação:
Encontrando esse ângulo poderemos obter .
Passo 2
Fazendo então primeiro
E a equação de se escreve:
Como
Como , a equação de será:
Passo 3
O esboço ficará:
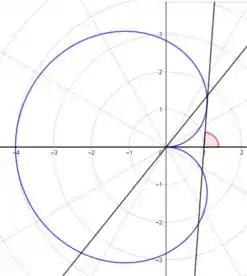
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Encontre os coeficientes angulares das curvas nos Exercícios 17-20 nos pontos determinados. Esboce as curvas com suas tangentes nesses pontos.Cardioide r = - 1 + sen θ ; θ = 0 ,π
Encontre os coeficientes angulares das curvas nos Exercícios 17-20 nos pontos determinados. Esboce as curvas com suas tangentes nesses pontos.Rosa de quatro pétalas r = cos 2 θ ; θ = 0 ,± π / 2 ,π
Encontre os coeficientes angulares das curvas nos Exercícios 17-20 nos pontos determinados. Esboce as curvas com suas tangentes nesses pontos.Cardioide r = - 1 + cos θ ; θ = ± π / 2
Encontre os coeficientes angulares das curvas nos Exercícios 17-20 nos pontos determinados. Esboce as curvas com suas tangentes nesses pontos.Rosa de quatro pétalas r = sen 2 θ ; θ = ± π / 4 ,± 3 π
Encontre equações paramétricas e um intervalo de parâmetro para o movimento de uma partícula no plano xy que trace a elipse 16x2 + 9y2 = 144 uma vez em sentido anti-horário. (Existem muitas formas de