Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.4 - Ex. 43

Nos exercícios de 39 a 44, ache a área da região, tomando como medida da altura do i - é s i m o retângulo   f ( m i ) , onde m i é o ponto médio do i - é s i m o subintervalo. Sugestão: m i = 1 2 x i + x i - 1 .

43. A região do Exercício 27.

Passo 1

A região do exercício 27 é:

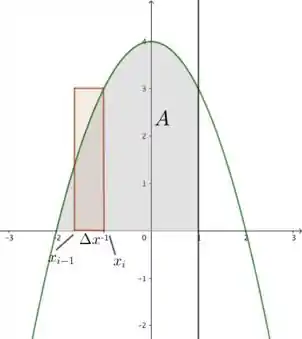
O intervalo da região será [ - 2,1 ] e a função é f x = 4 - x 2 . Sendo assim,

Δ x = 1 - ( - 2 ) n = 3 n

m i = 1 2 x i + x i - 1

f m i = 4 - 1 2 x i + x i - 1 ⏟ m i 2 = 4 - 1 4 - 2 + 3 i n + - 2 + 3 ( i - 1 ) n 2

f m i = 4 - 1 4 - 4 n + 3 i + 3 i - 1 n 2 = 4 - 1 4 6 i - ( 4 n + 1 ) n 2

= 16 n 2 - 36 i 2 - 12 4 n + 1 i + 4 n + 1 2 4 n 2

f m i = - 36 i 2 + 12 4 n + 1 i + 16 n 2 - 4 n + 1 2 4 n 2

A = lim n → + ∞ ⁡ ∑ i = 1 n f m i Δ x = lim n → + ∞ ⁡ ∑ i = 1 n - 36 i 2 + 12 4 n + 1 i + 16 n 2 - 4 n + 1 2 4 n 2 3 n  

lim n → + ∞ ⁡ 3 4 n 3 ∑ i = 1 n - 36 i 2 + 12 4 n + 1 i + 16 n 2 - 4 n + 1 2

A = lim n → + ∞ ⁡ 3 4 n 3 - 36 ∑ i = 1 n i 2 + 12 4 n + 1 ∑ i = 1 n i + 16 n 2 - 4 n + 1 2 ∑ i = 1 n 1

Passo 2

Agora vamos usar as fórmulas dos somatórios e calcular o limite.

∑ i = 1 n 1 ⏞ I = n                                 ∑ i = 1 n i ⏞ = I I n ( n + 1 ) 2                           ∑ i = 1 n i 2 ⏞ I I I = n ( n + 1 ) ( 2 n + 1 ) 6

A = lim n → + ∞ ⁡ 3 4 n 3 - 36 n ( n + 1 ) ( 2 n + 1 ) 6 + 12 4 n + 1 n ( n + 1 ) 2 + 16 n 2 - 4 n + 1 2 n

A = 3 4 lim n → + ∞ ⁡ - 36 n n 1 + 1 n 2 + 1 n 6 + 12 4 + 1 n n n 1 + 1 n 2 + 16 n 2 n 2 - 4 + 1 n 2 n n

A = 3 4 ⁡ - 36 1 + 0 2 + 0 6 + 12 4 + 0 1 + 0 2 + 16 - 4 + 0 2

A = 3 4 ⁡ - 72 6 + 12 ⋅ 4 2 + 12 = 3 4 ⁡ - 12 + 24 2 + 12 = 3 4 ⋅ 12 = 9

A = 9

Logo, a área é 9   u . a .

Resposta

A = 9   u . a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O gráfico da velocidade de um carro acelerado está mostrado a seguir.Dê uma estimativa da velocidade média do veículo durante os primeiros 12 segundos. Em que instante a velocidade instantânea foi igu
Quão grande deve ser n para garantir que a aproximação pela Regra de Simpson de ∫ 0 1 e x 2 d x tenha uma precisão de 0,00001 ?
Use (a) a Regra do Trapézio, (b) a Regra do Ponto Médio e (c) a Regra de Simpson para aproximar a integral dada com o valor especificado de n . (Arredonde seu resultado para seis casas decimais.) ∫ 4
Use (a) a Regra do Trapézio, (b) a Regra do Ponto Médio e (c) a Regra de Simpson para aproximar a integral dada com o valor especificado de n . (Arredonde seu resultado para seis casas decimais.) ∫ 0
Use (a) a Regra do Trapézio, (b) a Regra do Ponto Médio e (c) a Regra de Simpson para aproximar a integral dada com o valor especificado de n . (Arredonde seu resultado para seis casas decimais.) ∫ 0