Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.1 - Ex. 8

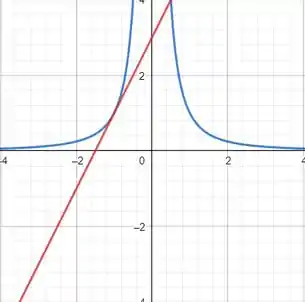
Nos Exercícios 5-10, determine uma equação para a tangente à curva em um ponto dado. Em seguida, esboce a curva e a tangente em um único gráfico.

y = 1 x 2 ,           ( - 1 , 1 )

Passo 1

Relembrando a equação da reta tangente :

y - f a = m x - a

Nesse caso,

y - 1 = m x + 1

Assim, precisamos determinar o m , que é o coeficiente angular da curva no ponto dado. Para isso, vamos usar a equação:

m = lim h → 0 ⁡ f x + h - f x h

Passo 2

A primeira coisa a ser feita é substituir a função f x na equação acima:

m = lim h → 0 ⁡ 1 x + h 2 - 1 x 2 h

Em seguida, vamos substituir na equação anterior o valor de x = - 1 .

m = lim h → 0 ⁡ 1 - 1 + h 2 - 1 - 1 2 h

m = lim h → 0 ⁡ 1 - 1 + h 2 - 1 h

Passo 3

Agora precisamos fazer o MMC na parte de cima da fração para facilitar as contas.

m = lim h → 0 ⁡ 1 - - 1 + h 2 - 1 + h 2 h = lim h → 0 ⁡ 1 - - 1 + h 2 h - 1 + h 2

Lembrando que - 1 + h 2 = 1 - 2 h + h 2 .

m = lim h → 0 ⁡ 1 - ( 1 - 2 h + h 2 ) h - 1 + h 2

m = lim h → 0 ⁡ 2 h - h 2 h - 1 + h 2

Cortando o termo h , ok?

m = lim h → 0 ⁡ 2 - h - 1 + h 2 = 2 - 0 - 1 + 0 2 = 2

Passo 4

Lembra da equação da tangente que definimos lá em cima, agora devemos substituir o valor encontrado de m .

y - 1 = m x + 1

y - 1 = 2 x + 1

Reescrevendo a equação:

y = 2 x + 3

Passo 5

Por fim, vamos desenhar a curva e a tangente encontrada.

Resposta

y = 2 x + 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontrar a derivada das funções dadas. A seguir, comparar os resultados encontrados com os resultados obtidos a partir do uso de um software algébrico. f t = t - 1 t + 1
Encontrar a derivada das funções dadas. A seguir, comparar os resultados encontrados com os resultados obtidos a partir do uso de um software algébrico. f x = 4 - x 5 - x 2
Encontrar a derivada das funções dadas. A seguir, comparar os resultados encontrados com os resultados obtidos a partir do uso de um software algébrico. f t = 2 - t 2 t - 2
Encontrar a derivada das funções dadas. A seguir, comparar os resultados encontrados com os resultados obtidos a partir do uso de um software algébrico. f t = 3 t 2 + 5 t - 1 t - 1
33-36. Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.33. Se f e g forem deriváveis em x = 2 , então: d d x f x - 8 g x x = 2 = f ' 2 - 8 g ' 2