Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 4.12 - Ex. 29
Em que ponto o gráfico da função tem tangente horizontal?. Esboçar o gráfico e analisar o resultado obtido.
Passo 1
Podemos calcular o coeficiente angular de uma reta tangente usando a definição da derivada de uma função, em que o coeficiente da reta tangente é a derivada da função no ponto desejado. Ou seja:
Onde representa o ponto desejado.
Em uma reta horizontal, seu coeficiente de inclinação é . Da mesma forma que podemos encontrar o coeficiente angular da reta tangente fazendo a derivada da função e aplicando no ponto, podemos encontrar o ponto quando igualamos a derivada da função ao seu coeficiente angular.
Passo 2
Temos que calcular então a derivada da curva . Assim temos:
A derivada de é
Passo 3
O coeficiente da reta tangente será . Com o coeficiente angular, podemos encontrar os pontos pelo qual essas retas tangentes passam. Para isso igualamos o coeficiente com a primeira derivada da curva:
Resolvendo por Bhaskara temos os pontos que satisfazem essa equação é quando: e .
Substituindo na equação da curva, teremos os pontos em que a curva tem tangente horizontal.
Para :
Temos então que uma reta tangente passa pelo ponto .
Para :
Temos então que a outra reta tangente passa pelo ponto .
Passo 4
O gráfico da função e das retas tangentes e paralela é o seguinte:
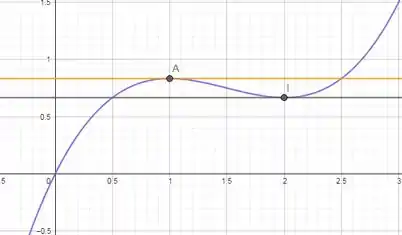
Podemos perceber nesse gráfico que as retas tangentes passam por pontos de máximo e mínimo locais da função. Ou seja, toda vez que derivarmos uma função e igualamos a zero, vamos estar procurando pontos de máximo e mínimo na uma função.
Resposta
Ponto
Ponto