Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 9.3 - Ex. 10

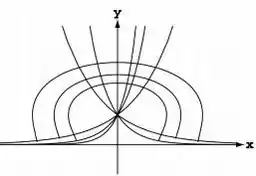
Nos Exercícios 5-10, determine as trajetórias ortogonais da família de curvas. Esboce vários membros de cada família.

10 - y = e k x

Passo 1

y = e k x ⇒ ln ⁡ y = k x

Logo:

k = ln ⁡ y x

Assim derivando:

x 1 y y ' - ln ⁡ y x 2 = 0

x 1 y y ' - ln ⁡ y = 0

x y y ' = ln ⁡ y

y ' = ln ⁡ y x y

y ' = y ln ⁡ y x

Para a ortogonalidade, teremos:

d y d x = - x y ln ⁡ y

Assim:

y ln ⁡ y   d y = - x   d x

Precisaredmos integrar a função:

∫ y ln ⁡ y   d y = ∫ - x d x

A s s i m :

y 2 2 ln ⁡ y - 1 4 y 2 = - x 2 2 + c

Poderemos simplificar se multiplicarmos toda a expressão por 2:

y 2 ln ⁡ y - y 2 2 = - x 2 + C

Resposta

y 2 ln ⁡ y - y 2 2 = - x 2 + C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 5-10, determine as trajetórias ortogonais da família de curvas. Esboce vários membros de cada família. y = m x
Percurso de uma bicicleta um ciclista de 66 kg em uma bicicleta de 7 kg inicia seu percurso no nível do solo a 9 m/s. O k na Equação 1 é de cerca de 3,9 kg/s.b-Após quanto tempo, aproximadamente, a ve
Percurso de uma bicicleta Um ciclista de 66 kg em uma bicicleta de 7 kg inicia seu percurso no nível do solo a 9 m/s. O k na Equação 1 é de cerca de 3,9 kg/s.b-Quanto tempo levará para a velocidade do
Os dados na Tabela 9.4 foram coletados com um detector de movimento e um CBLTM ( computer based learning - aprendizagem assistida por computador) por Valerie Sharritts, uma professora de matemática da
Deslizando até parar A Tabela 9.5 mostra a distância s ( em metros) em termos do instante t (em segundos) que Kelly Schmitzer percorreu de patins. Determine mn modelo para a sua posição na forma da Eq