Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.7 - Ex. 11

Nos exercícios de 9 a 12, ache a área da região limitada por um laço do gráfico da equação dada.

11.

Passo 1

O enunciado nos da a equação de um gráfico e pede para determinarmos a área. Para isso, primeiro é ideal fazer o esboço do gráfico da equação dada para observar quais são os limites de . Após fazer o esboço da equação , podemos utilizar o que foi mostrado ao longo da seção quando queremos saber a área de uma região dada em coordenadas polares, que nos diz que para calcular a mesma podemos utilizar que a área da região é : .

Em muitos problemas também podemos utilizar o conceito de simetria.

Passo 2

Assim, o esboço do gráfico da equação dada é:

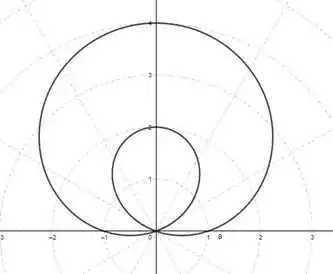
Como ele quer a área de um laço somente, basta fazer variar de ; e por ser simétrico em relação ao semi-eixo, basta multiplicar por 2 para encontrar o valor da área de um laço.