Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.Revisão - Ex. 58
Nos exercícios de 57 a 62, faça um esboço do gráfico da função; então, observando as quebras no gráfico, determine os valores da variável independente nos quais a função é descontínua e mostre, em cada caso de descontinuidade, por que a Definição 2,6,1 não é satisfeita.
58)
Passo 1
As assíntotas horizontais são obtidas quando fazemos x tender a mais infinito e a menos infinito.
Lembrando que, limites de funções polinomiais quando x tende a infinito, tomamos o termo dominante no numerador e no denominador.
Portanto, teremos uma assíntota horizontal em .
Passo 2
As assíntotas verticais são obtidas calculando os limites laterais nas restrições do domínio da função.
O domínio da função é:
Calcularemos os limites a direita e esquerda do 1 e do -2:
Portanto, teremos “bolinha aberta” em .
Passo 3
O gráfico da função será:
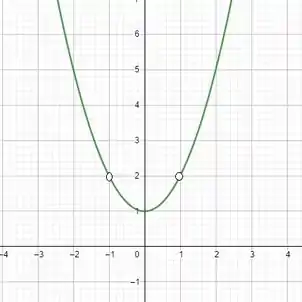
Passo 4
Agora vamos verificar as condições da Definição 2.6.1
- não existem
Portanto, como uma das condições não foram verificadas, a função é descontinua em 1 e em -1.
Resposta
Gráfico da função:
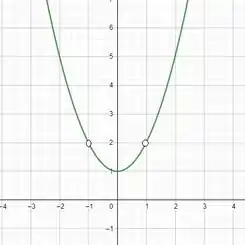
A função é descontínua em