Enunciado
Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.2 - Ex. 66
Nos Exercícios de 61 a 66, use Geometria Analítica para provar o teorema dado a partir da Geometria Plana.
Se as diagonais de um quadrilátero dividem-se ao meio, então o quadrilátero é um paralelogramo.
Passo 1
Para começar, precisamos lembrar que paralelogramo são quadriláteros que apresentam lados opostos congruentes e paralelos.
Vamos imaginar um quadrilátero cujos vértices são A(0,0), B (0,b), C (a,b) e D (a,0). Calculando o ponto médio para cada uma das diagonais AC e BC:
Para AC ():
Para BD ():
Sendo assim, as diagonais possuem seu ponto médio em comum indicando que se cruzam neste ponto, ou seja, se dividem ao meio.
Passo 2
Vimos que as diagonais se dividem ao meio, agora precisamos provar que os lados opostos são congruentes e paralelos.
Ilustrando a situação:
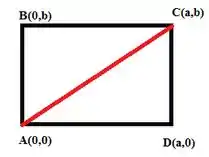
Para saber se os lados opostos são realmente paralelos, precisamos calcular a distância entre os pontos para saber se são congruentes.
Reta
Reta oposta CD
Se analisarmos o desenho vamos perceber que a diagonal divide o quadrilátero em dois triângulos, ABC e ACD. Como a diagonal é a mesma e os lados AB e CD são iguais, temos triângulos congruentes pelo caso LLL (Lado-Lado-Lado). Concluímos então que:
Se os triângulos são congruentes, temos os três ângulos são iguais para cada triângulo:
Segundo o teorema dos ângulos alternos internos, quando uma diagonal cruza duas retas paralelas os ângulos alternos internos possuem posição alternada na região interna e são congruentes. Como é o que ocorre no nosso problema podemos concluir que AD é paralela a BC. A mesma análise pode ser feita e comprovar que AB é paralela a CD.
Comprovamos que lados opostos são paralelos e congruente, ou seja, temos um paralelogramo.
Resposta
Ei, a resposta está no passo a passo :)