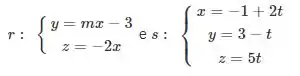Exercícios de Posições Relativas de Retas - Lista de Exercícios Resolvida

Calcular o valor de para que as retas

Sejam ortogonais.

Calcular o valor de para que os seguintes pares de retas sejam paralelas:

1. e
2. e

Ache equações paramétricas da reta que passa por e é perpendicular à reta

Estude a posição relativa das retas:

e

Verifique se as retas

são ortogonais. Verifique também se são perpendiculares.

Mostre que as retas abaixo são concorrentes e determine o ponto de interseção entre elas.

e

Sejam e as retas reversas, passando por e e por e respectivamente. Obtenha uma equação vetorial da reta , concorrente com e , e paralela ao vetor .

Dados: e .

Estude a posição relativa das retas

e

Duas retas e coplanares e não paralelas são concorrentes. Consideremos as retas:

e

Determinemos seu ponto de interseção.

Em , seja t a reta que passa pelo ponto e é concorrente com as retas

Se é um vetor diretor de t, então é igual a

Considere as retas e

a) Escreva equações paramétricas para a reta .

b) Mostre que e são concorrentes.

c) Escreva equações paramétricas para a reta que corta e perpendicularmente.

Considere as retas concorrentes r e s dadas respectivamente pelas equações:

Se for o ponto na interseção de r e s, então será igual a:

Seja tal que as retas

São concorrentes. Sabendo-se que é a interseção entre elas, corretor afirmar que é igual a:

Sejam e considere as retas:

Temos que e são reversas se, e somente se:

Em , seja o plano que contém o ponto e a reta de equação . A equação da reta perpendicular a e que passa pelo ponto é:

Em , seja r a reta de equação e s a reta de equação

Então a distância entre r e s vale

Sabe-se que é vértice de um quadrado que possui uma diagonal contida na reta . Então é correto afirmar que existe um outro vértice do quadrado com igual a:

Em , considere o ponto , a reta r de equação e o plano . Seja P o ponto de interseção da reta r com o plano que passa por A e é paralelo a . É correto afirmar que é igual a:

Considere as retas e dadas respectivamente pelas equações:

e

Se for a reta perpendicular comum a e e se for o ponto da intersecção de e , então será igual a:

a) ;

b)

c) ;

d)

e)

03) Seja . A cônica de equação é um par de retas concorrentes se, e somente se, for igual a:

A)

B)

C)

D)

E)

Sejam as retas e .

a) Determine a posição relativa entra as retas e .

b) Determine as equações paramétricas para a reta perpendicular comum às retas e .

Considere as retas e de cujas equações paramétricas são

A reta de equação cartesiana

E o plano de equação cartesiana

a) Determine o valor de para que as retas e se interceptem em um ponto. Nesse caso (para o valor de obtido) determine o ponto de interseção das retas e .

Em , as retas

São concorrentes com a reta h nos pontos A, B, e C, respectivamente. Se é o ponto médio do segmento AC, então é igual a

A equação da reta em paralela à direção do vetor e que passa pelo ponto é:

Sejam tais que , e tais que a medida do ângulo entre e seja igual a . Temos que a equação:

Na incógnita real tem duas soluções distintas. A soma dessas duas soluções é igual a:

a)

b)

c)

d)

e)

Considere o plano dado pela equação:

e seja o ponto simétrico ao ponto em relação a , isto é, o ponto tal que o vetor seja ortogonal a e o ponto médio do segmento esteja em . Temos que é igual a:

a)

b)

c)

d)

e)