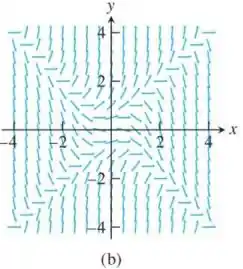
Nos Exercícios 1-4, associe as equações diferenciais a seus campos de direção, representados a seguir.
Passo 1
Para descobrir qual é o campo de direção que representa a equação dada, pode-se fazer a análise para cada valor de e a fim de determinar qual é o comportamento das curvas.
Como a equação é a derivada de uma função, ela também representa a inclinação de uma determinada curva em cada ponto que poderá ser nula, positiva ou negativa.
Passo 2
Assim, é possível analisar diversas combinações de valores para as variáveis.
Para e , a inclinação é nula;
Para , a inclinação é positiva;
Para , a inclinação é negaitiva.

Passo 3
Com essas informações é possível concluir que o campo de direção (b) representa a equação dada.
Resposta