Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.6 - Ex. 14

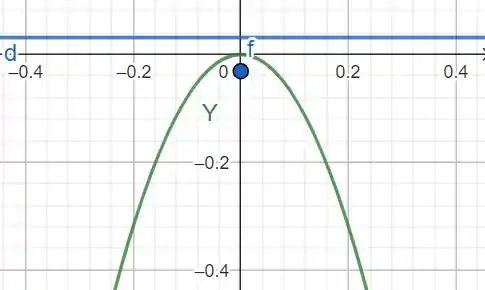
Os Exercícios 9-16 dão equações de parábolas. Encontre o foco e a diretriz de cada uma das parábolas. Em seguida, esboce a parábola. Inclua o foco e a diretriz em seu esboço.

y = - 8 x 2

Passo 1

Fala gente tudo bem? Como quem está ao quadrado é o x, essa equação representa uma parábola horizontal, dessa forma, vamos utilizar as fórmulas que aprendemos nessa seção para encontrar o ponto p:

y = - 8 x 2 ⇒ y = x 2 - 1 8 = x 2 4 p

4 p = - 1 8 → p = - 1 32

O foco então é 0 , p = ( 0 , - 1 32 ) e a diretriz é y = - p = 1 32 .

Passo 2

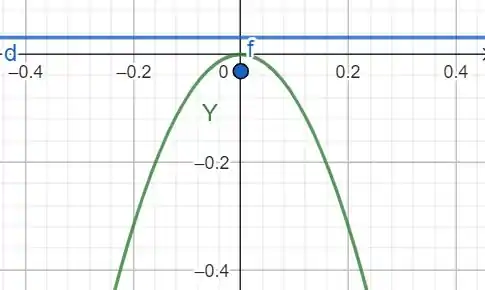Vamos desenhar utilizando nosso querido Geogebra:

Bora pro próximo.

Resposta

0 , - 1 32 e a diretriz é y = 1 32 .

Exercícios de Livros Relacionados

Os Exercícios 45-48 fornecem equações para parábolas e nos dize quantas unidades para cima ou para baixo e para direita ou para esquerda cada parábola deve ser deslocada. Encontre uma equação para a n
Os Exercícios 45-48 fornecem equações para parábolas e nos dize quantas unidades para cima ou para baixo e para direita ou para esquerda cada parábola deve ser deslocada. Encontre uma equação para a n
Os Exercícios 45-48 fornecem equações para parábolas e nos dize quantas unidades para cima ou para baixo e para direita ou para esquerda cada parábola deve ser deslocada. Encontre uma equação para a n
A parábola X2 = -4y é deslocada 1 unidades para esquerda e 3 unidade para cima para gerar a parábola (x+1)=4(y-3) a. Encontre o vértice, foco e diretriz da nova parábola.b. Represente graficamente os
A parábola y2 = 8x é deslocada 2 unidades para baixo e 1 unidade para a direita para gerar a parábola (y + 2)2 = 8(x - 1). a. Encontre o vértice, foco e diretriz da nova parábola.b. Represente grafica