Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.6 - Ex. 17

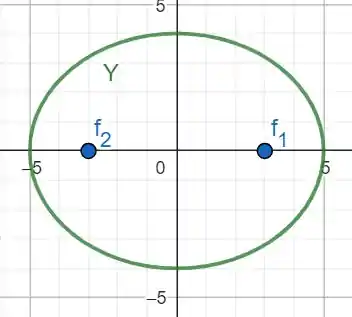
Os Exercícios 17-24 nos dão equações para elipses. Coloque cada uma das equações na forma padrão. Em seguida, esboce a elipse. Inclua os focos em seu esboço.

16 x 2 + 25 y 2 = 400

Passo 1

Fala gente tudo bem? Primeiramente devemos colocar nas formas padrão, ou seja, encontrar os denominadores a e b da equação, lembrando sempre que a > b .

x 2 a 2 + y 2 b 2 = 1   o u   x 2 b 2 + y 2 a 2 = 1  

16 x 2 + 25 y 2 = 400

16 x 2 16 ⋅ 25 + 25 y 2 16 ⋅ 25 = 400 16 ⋅ 25

x 2 25 + y 2 16 = 1

Passo 2

Para encontrar os focos precisamos encontrar o ponto c:

c = a 2 - b 2

c = 25 - 16

c = 9 = ± 3

Passo 3

Vamos desenhar utilizando nosso querido Geogebra:

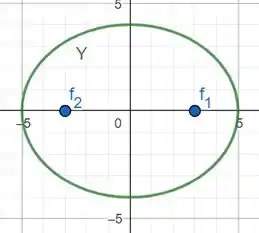
Bora pro próximo.

Resposta

x 2 25 + y 2 16 = 1

Exercícios de Livros Relacionados

Os Exercícios 13-16 fornecem os focos e as diretrizes correspondentes das elipses centradas na origem do plano xy. Em cada um dos casos, utilize as dimensões na Figura 11.45 para encontrar a excentric
Os Exercícios 25 e 26 nos dão informações sobre os focos e vértices das elipses centradas na origem do plano xy. Em cada um dos casos, encontre a equação na forma padrão da elipse a partir das informa
Os Exercícios 49-52 fornecem equações para elipses e nos dizem quantas unidades para cima ou para baixo e para a direita ou para a esquerda cada elipse deve ser deslocada. Encontre uma equação para a
Os Exercícios 27-34 fornecem equações para hipérboles. Coloque cada equação na forma padrão e encontre as assíntotas da hipérbole. Em seguida, esboce a hipérbole. Inclua as assíntotas e focos no seu e
Os Exercícios 35-38 fornecem informações sobre os focos, vértices e assíntotas de hipérboles centradas na origem do plano xy. Em cada um dos casos, encontre a equação na forma padrão da hipérbole a pa