Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 13.Exercícios práticos - Ex. 1

Nos Exercícios 1 e 2, desenhe as curvas e esboce seus vetores velocidade e aceleração nos valores fornecidos de t. Em seguida, escreva a na forma a = a T T + a N N sem determinar T e N e encontre o valor de κ nos valores determinados de t.

r t = 4 cos ⁡ t i + 2 s e n   t j ,   t = 0   e   π 4

Passo 1

E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de funções vetoriais e movimentos no espaço.

Vamos agora resolver os exercícios práticos sobre movimento no plano.

A partir do enunciado temos que:

x = 4 cos ⁡ t   e   y = 2 s e n   t

De onde podemos perceber que:

a = 4   e   b = 2

Logo, teremos a equação da elipse:

x 2 a 2 + y 2 b 2 = 1 = > x 2 16 + y 2 2 = 1

E derivando r:

v t = d r t d t = - 4 s e n   t i + 2 cos ⁡ t j

a t = d v t d t = - 4 cos ⁡ t i + - 2 s e n   t j

Passo 2

Para t = 0 teremos:

r 0 = 4 cos ⁡ 0 i + 2 s e n   0 j = 4 i

v 0 = - 4 s e n   0 i + 2 cos ⁡ 0 j = 2 j

a 0 = - 4 cos ⁡ 0 i + - 2 s e n   0 j = - 4 i

Para t = π/4 teremos:

r π 4 = 4 cos ⁡ π 4 i + 2 s e n   π 4 j = 2 2 i + j

v π 4 = - 4 s e n   π 4 i + 2 cos ⁡ π 4 j = - 2 2 i + j

a π 4 = - 4 cos ⁡ π 4 i + - 2 s e n   π 4 j = - 2 2 i - j

Passo 3

Lembrando que:

a T = d d t v ,   a N = a 2 - a T 2   e   κ = a N v 2

Fazemos:

v = - 4 s e n   t 2 + 2 cos ⁡ t 2 = 16 s e n 2   t + 2 cos 2 ⁡ t

a = - 4 cos ⁡ t 2 + - 2 s e n   t 2 = 16 cos 2 ⁡ t + 2 s e n 2 t

Daí, temos que:

a T = d d t v = d d t 16 s e n 2   t + 2 cos 2 ⁡ t = 14 s e n   t cos ⁡ t 16 s e n 2   t + 2 cos 2 ⁡ t

Em t = 0 teremos:

a T = 0   e   a N = a 2 - 0 = 16 cos 2 ⁡ 0 + 2 s e n 2   0 2 = 16 = 4

= > a = 0 T + 4 N   e   κ = 4 16 s e n 2   0 + 2 cos 2 ⁡ 0 2 = 4 2 = 2

Passo 4

De forma similar, em t = π/4 teremos:

a T = 14 s e n   π 4 cos ⁡ π 4 16 s e n 2   π 4 + 2 cos 2 ⁡ π 4 = 14 ∙ 2 2 ∙ 2 2 16 ∙ 1 2 + 2 ∙ 1 2 = 7 8 + 1 = 7 3

a N = a 2 - 7 3 2 = 16 cos 2 ⁡ π 4 + 2 s e n 2   π 4 2 - 49 9 = 16 ∙ 1 2 + 2 ∙ 1 2 - 49 9 = 8 + 1 - 49 9 = 81 - 49 9 = 32 9 = 4 2 3

= > a = 7 3 T + 4 2 3 N   e   κ = 4 2 3 16 s e n 2   π 4 + 2 cos 2 ⁡ π 4 2 = 4 2 3 16 ∙ 1 2 + 2 ∙ 1 2 = 4 2 3 9 = 4 2 27

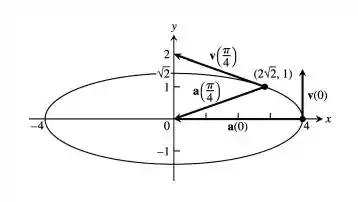
E é isso pessoal. Espero que a resolução tenha sido proveitosa para todos. Até mais.

Resposta

Ver passo a passo.

Exercícios de Livros Relacionados

Calcule os limites. lim t → 0 + ⁡ cos ⁡ t ,s e nt ,t ln ⁡ t
Módulo de velocidade ao longo de uma cicloideUma roda circular com raio de 1 pé e centro C gira para a direita ao longo do eixo x a meia-volta por segundo. (Veja a figura a seguir.) No tempo t segundo
Uma bola de golfe é atingida com uma velocidade inicial v0 a um ângulo α em relação à horizontal a partir de um ponto localizado na base de um morro inclinado a um ângulo ϕ com a horizontal, em que 0φ
Nos Exercícios 17-20, encontre T, N, B, κ e τ no valor determinado de t. r t = 4 9 1 + t 3 / 2 i + 4 9 1 - t 3 / 2 j + 1 3 t k ;t = 0