Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 13.Exercícios práticos - Ex. 13

Uma bola de golfe é atingida com uma velocidade inicial v0 a um ângulo α em relação à horizontal a partir de um ponto localizado na base de um morro inclinado a um ângulo ϕ com a horizontal, em que

0 < φ < α < π 2

Mostre que a bola toca o solo a uma distância

2 v 0 cos ⁡ α g cos 2 ⁡ φ s e n α - φ

medida da base do morro. Consequentemente, mostre que a maior distância que pode ser alcançada para determinado valor de v0 ocorre quando α = φ 2 + π 4 , ou seja, quando o vetor velocidade inicial bissecta o ângulo entre a vertical e o morro.

Passo 1

E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de funções vetoriais e movimentos no espaço.

Vamos agora resolver os exercícios práticos sobre movimento de projéteis.

A partir do enunciado, teremos:

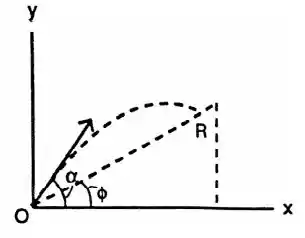
Escrevendo as equações do movimento, temos:

x = v 0 cos ⁡ α t   e   y = v 0 s e n   α t - 1 2 g t 2

Daí temos que:

t g   φ = y x = v 0 s e n   α t - 1 2 g t 2 v 0 cos ⁡ α t = v 0 s e n   α - 1 2 g t v 0 cos ⁡ α

Isolando t obtemos:

v 0 cos ⁡ α   t g   φ = v 0 s e n   α - 1 2 g t = > t = 2 g v 0 s e n   α - v 0 cos ⁡ α   t g   φ

Que é o momento em que a bola de golfe atinge a inclinação ascendente.

Passo 2

Neste tempo teremos:

x = v 0 cos ⁡ α 2 g v 0 s e n   α - v 0 cos ⁡ α   t g   φ = 2 g v 0 2 s e n   α cos ⁡ α - v 0 2 cos 2 ⁡ α   t g   φ

Sabemos também que:

x = O R cos ⁡ φ = > O R = 2 g v 0 2 s e n   α cos ⁡ α - v 0 2 cos 2 ⁡ α   t g   φ cos ⁡ φ

Simplificando, obtemos:

O R = 2 v 0 2 cos ⁡ α g s e n   α cos ⁡ φ - cos ⁡ α   t g   φ cos ⁡ φ = 2 v 0 2 cos ⁡ α g s e n   α   cos ⁡ φ - cos ⁡ α   s e n   φ cos 2 ⁡ φ =

= 2 v 0 2 cos ⁡ α g s e n α - φ cos 2 ⁡ φ = 2 v 0 cos ⁡ α g cos 2 ⁡ φ s e n α - φ

Passo 3

Para maximizarmos o segmento OR fazemos:

d x d α = 0 = > 2 v 0 2 g cos ⁡ 2 α + s e n   2 α   t g   φ = 0

= > cos ⁡ 2 α + s e n   2 α   t g   φ = 0 = > c o t g   2 α + t g   φ = 0

= > c o t g   2 α = - t g   φ = t g - φ = > 2 α = π 2 + φ = > α = φ 2 + π 4

E é isso pessoal. Espero que a resolução tenha sido proveitosa para todos. Até mais.

Resposta

Ver passo a passo.

Exercícios de Livros Relacionados

A posição de uma partícula no plano no tempo t é r = 1 1 + t 2 i + t 1 + t 2 j Encontre o módulo de velocidade mais alto da partícula.
Lançamento de pesoUm peso sai da mão do arremessador a 6,5 pés acima do solo a um ângulo de 45º e a 44 pés/s. Onde o peso estará 3 segundos depois?
DardoEm Postdam, em 1988, Petra Felke da (então) Alemanha Oriental, quebrou o recorde mundial feminino arremessando um dardo a 262 pés e 5 pol.Considerando que Felke lançou o dardo a um ângulo de 40º
DardoUm dardo sai da mão do arremessador a 7 pés acima do solo a um ângulo de 45º e a 80 pés/s. Qual é a sua altura máxima alcançada?
Encontre o ponto na curva y = e x , em que a curvatura máxima é alcançada.