Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 13.Exercícios práticos - Ex. 10

Módulo de velocidade ao longo de uma cicloide

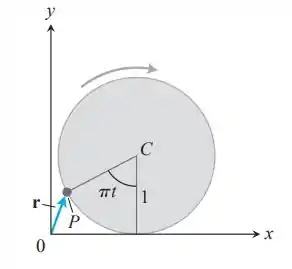
Uma roda circular com raio de 1 pé e centro C gira para a direita ao longo do eixo x a meia-volta por segundo. (Veja a figura a seguir.) No tempo t segundos, o vetor posição do ponto P na circunferência da roda é

r = π t - s e n   π t i + 1 - cos ⁡ π t j

  1. Esboce a curva traçada por P durante o intervalo 0 ≤ t ≤ 3 .
  2. Encontre v e a em t = 0, 1, 2 e 3 e adicione esses vetores ao seu esboço.
  3. Em qualquer instante determinado, qual é o módulo de velocidade de avanço do ponto mais alto da roda? E de C?

Passo 1

E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de funções vetoriais e movimentos no espaço.

Vamos agora resolver os exercícios práticos sobre movimento no plano.

Item a

A partir do enunciado, teremos um esboço:

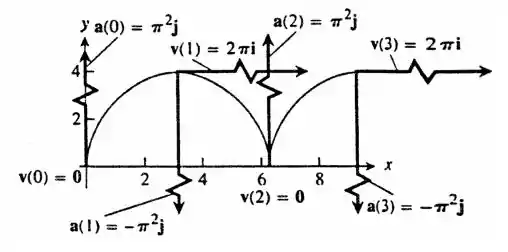
Obs.: O esboço foi pedido no item a, mas deveria ser pedido no último item da questão, pois os cálculos necessários para esboças serão realizados no item b.

Passo 2

Item b

Derivando r:

d r d t = v = π - π cos ⁡ π t i + π s e n   π t j

E:

d v d t = a = π 2 s e n   π t i + π 2 cos ⁡ π t j

Para os valores de t no intervalo pedido temos:

v 0 = 0 ; v 1 = 2 π i ; v 2 = 0 ; v 3 = 2 π i

a 0 = π 2 j ;   a 1 = - π 2 j ; a 2 = π 2 j ; a 3 = - π 2 j ;

Passo 3

Item c

A velocidade de avanço no ponto mais alto é:

v ( 1 ) = v ( 3 ) = 2 π   p é s / s

Como o círculo faz 1/2 volta por segundo, o centro se move em π pés, paralelo ao eixo x a cada segundo. A velocidade de avanço de C é:

π   p é s / s

E é isso pessoal. Espero que a resolução tenha sido proveitosa para todos. Até mais.

Resposta

Ver passo a passo.

Exercícios de Livros Relacionados

Suponha que r seja o vetor posição de uma partícula que se move ao longo de uma curva plana e dA/dt seja a taxa na qual o vetor varre a área. Sem introduzir coordenadas e assumindo que as derivadas ne
Terceira lei de KeplerComplete a dedução da terceira lei de Kepler (a parte seguinte à Equação 10).
Caracterizando o movimento circularUma partícula se move no plano de forma que seus vetores de velocidade e posição são sempre ortogonais. Mostre que a partícula se move em um círculo centrado na orig
Suponha que r ( t ) = e t cos ⁡ t i + e t s e nt j . Mostre que o ângulo entre r e a nunca muda. Qual é o ângulo?
Uma partícula se move ao redor de um círculo unitário no plano xy. Sua posição no tempo t é r = x i + y j , em que x e y são funções deriváveis de t. Encontre dy/dt se v ∙ i = y . O movimento é em sen