Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.Exercícios práticos - Ex. 5
Os Exercícios 1-6 fornecem equações paramétricas e intervalos paramétricos para o movimento de uma partícula no plano . Identifique a trajetória da partícula encontrando uma equação cartesiana para ela. Desenhe a equação cartesiana e indique a direção do movimento e a porção traçada pela partícula.
Passo 1
Salve, fera! Tudo bem? Essa questão pode não ser tão simples. Vamos encará-la juntos?
Nesse problema iremos começar transformando a equação parametrizada em equação cartesiana para podermos compreendê-la melhor e podemos traçar o seu gráfico.
Simbora?
Passo 2
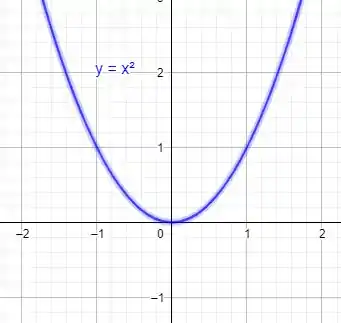
Como então logo ou ainda .
Esta é a equação de uma parábola com vértice na origem e concavidade para cima.
Seu gráfico será dado por:
Espero ter ajudado! Abraços e até a próxima!
Resposta
Veja a explicação acima.