Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 14.7 - Ex. 67
Nos Exercícios 66-68, utilize as Equações 2 e 3 para encontrar a reta
de mínimos quadrados para cada conjunto de pontos de dados. Em
seguida, utilize a equação linear obtida para prever o valor de y que
iria corresponder a x = 4
(–1, 2), (0, 1), (3, – 4)
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
Neste exercício nos é exposto um contexto sobre o método dos mínimos quadrados e regressão linear. Então, é pedido para usar as equações encontradas para definir a regressão pelo método dos mínimos quadrados para o conjunto de pontos abaixo.
Depois, vamos usar a equação da reta para fazer uma previsão do valor de que corresponde a Os pontos informados são: Vamos aos cálculos? Acompanhe!
Passo 2
Faremos o seguinte quadro para auxiliar na resolução:
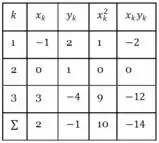
Passo 3
A aplicação das equações (2) e (3) do exercício 65 do tópico resultará em:
Então, a equação da reta é dada como:
Substituindo chegamos à resposta de:
Resposta
Resposta nos passos.