Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.7 - Ex. 50
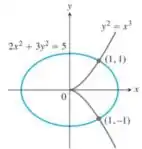
50. Existe algo especial em relação às tangentes das curvas e nos pontos ? Justifique sua resposta.
Passo 1
Antes de tudo, vamos denominar as funções da seguinte forma:
Agora que facilitamos a visualização das funções, como a questão fala de retas tangentes, então teremos que derivar implicitamente ambas as funções, ok? Lembrando que para derivarmos implicitamente, temos que lembrar dos passos:
1. Derivar ambos os lados da equação em relação a , considerando como uma função derivável de ;
2. Agrupar os termos que possuem em um lado da equação e isolar .
Então bora lá!
Passo 2
Derivando a , temos:
Substituindo o primeiro ponto :
Substituindo o segundo ponto :
Passo 3
Derivando agora a , temos:
Substituindo o primeiro ponto :
Substituindo o primeiro ponto :
Passo 4
Então galera, com os resultados foi possível notar que o valor da derivada nos dois pontos deram valores opostos. Quando isso ocorre, isso implica que as retas nos dois pontos são perpendiculares entre si em seus pontos de intersecção. Para as duas funções isso ocorre.
O resultado fica ainda mais nítido se olharmos para o gráfico que nos foi cedido no enunciado.
Resposta
Ei, a resposta está no passo a passo :)