Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.1 - Ex. 36
(i) Explique por que a função f tem um ou mais buracos em seu gráfico e estabeleça os valores de x nos quais esses buracos ocorrem. (ii) Determine uma função g cujo gráfico seja idêntico ao de f, mas sem os buracos.
(35)
Passo 1
(i) Primeiro, vamos entender o que são esses buracos que o enunciado fala.
Esses buracos são os lugares onde a função não está definida, ou seja, onde a imagem não está definida. Isso acontece, geralmente, graças a valores de onde vamos ter divisões por ou raiz quadrada de número negativo.
No nosso caso ali, temos . Como não temos uma raiz nessa função, os buracos vão existir se houver alguma divisão por , ou seja, se:
.
Olhando para a equação, podemos ver que ela será quando , apenas!! Pois é o único valor que possui módulo .
Beleza! Então já resolvemos o primeiro item!
Passo 2
(ii) Para determinar a função com o gráfico idêntico, mas sem buracos, é simples: vamos apenas simplificar alguns termos da função original! Então:
Mas antes, vamos escrevê-la como uma função definida por partes. Para isso, devemos lembrar que temos que estudar a função quando (pegando valores positivos de ) e quando (pegando valores negativos de ). Vamos lá!
Quando :
Quando :
Logo:
Passo 3
Agora, sim, vamos olhar para cada condição e simplificar!
Primeiro, para :
Podemos simplificar o :
Agora, para :
Assim, vamos simplificar :
Trocando o sinal de tudo:
Com isso:
Agora, não temos buracos!! O gráfico dela é:
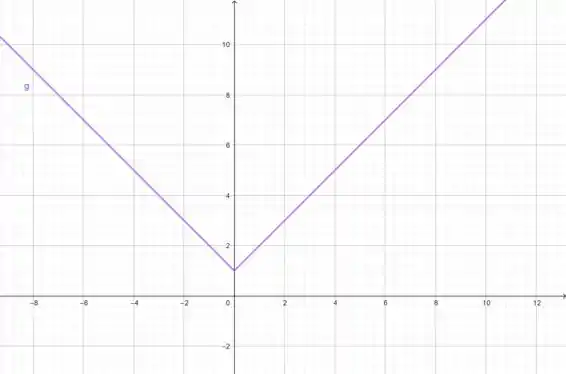
Resposta
(i)
(ii)