Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.1 - Ex. 67
- Faça o gráfico das funções e juntas para identificar os valores de para os quais
- Confirme algebricamente sua resposta no item
Passo 1
Esta é uma questão que necessita de recursos tecnológicos para ser resolvida. Sendo assim, utilizaremos de softwares para obtermos o gráfico da função. Após obtermos estes gráficos, vamos visualizar a informação que a inequação nos diz. Após isto, para provar algebricamente o que descobrimos na letra , vamos ter de desenvolver a inequação, e assim descobrir quais os valores de que as satisfazem.
Passo 2
Vamos começar por obter o gráfico das funções dos dois membros, isto é:
Observe abaixo o gráfico das duas funções.
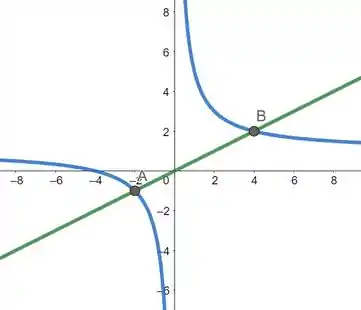
A inequação nos pede para encontrar os valores de tais que a função (em verde) é maior que a função (em azul). Graficamente isto corresponde aos pontos em que a curva verde está acima da azul. Desta forma, estes pontos correspondem ao intervalo do ponto até e do ponto até o . Portanto, como as coordenadas do ponto são e as do ponto são , valores estes obtidos graficamente, a solução da inequação é:
Passo 3
Agora, vamos provar matematicamente. Então, temos:
Para resolvermos esta inequação, vamos utilizar a seguinte ideia: a divisão de dois números negativos é um número positivo enquanto a divisão de um número negativo por um positivo é um número negativo. Esta ideia é a base do que iremos fazer. Vamos determinar os intervalos em que cada uma das funções , e são positivas e negativas. Depois, vamos multiplicar o sinal de cada uma delas. Se o resultado for negativo, a inequação toda será menor que zero. Caso contrário, será maior que zero. Vejamos então todos estes sinais na seguinte tabela:
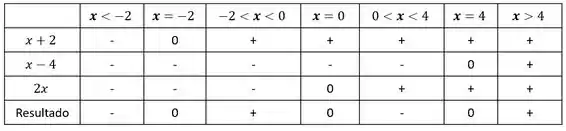
Portanto, a solução da inequação é: