Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.4 - Ex. 34
Faça o gráfico para dois períodos da função
Passo 1
Inicialmente, será necessário identificar qual o intervalo da função que contém quatro períodos. Funções cotangentes do tipo possui um período dado por:
Após a determinação do valor de , basta obter o gráfico em um intervalo de amplitude igual a .
Passo 2
Vamos inicialmente determinar a amplitude da função. Assim temos:
Passo 3
Como queremos um intervalo contendo 2 períodos, a amplitude do intervalo deve ser igual a:
Logo, a amplitude deve ser igual a . Então, o intervalo plotado será de
Passo 4
Obtendo o gráfico, temos:
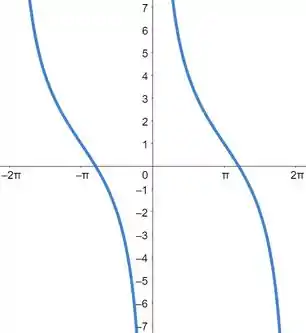
Resposta
Exercícios de Livros Relacionados
Dada f (x) = 2 x^2 + 5 x - 3 , ache f (3) .
Determine o domínio e a imagem da função e desenhe um esboço de seu gráfico. f x = 3 - x
Determine o domínio e a imagem da função e desenhe um esboço de seu gráfico. f x = 3 - x
Determine o domínio e a imagem da função e desenhe um esboço de seu gráfico. g x = x 2 + 2 x - 8 x - 2
Determine o domínio e a imagem da função e desenhe um esboço de seu gráfico. G x = x + 4 , s ex ≠ 2 1 , s ex = 2