Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.3 - Ex. 2
Explique como obter, a partir do gráfico de , os gráficos a seguir:
Passo 1
Boa galera, essa questão aqui é sobre transformações de gráfico de funções a partir de constantes.
Nela a gente vai ter que saber quando deslocar, refletir e expandir certa função para chegar em outra, então bora lá!
Primeiro vamos dar uma olhada em como as constantes afetam o gráfico de uma função:
Suponha que :
- , desloca o gráfico de em unidades para cima;
- , desloca o gráfico de em unidades para baixo;
- , desloca o gráfico de em unidades para direita;
- , desloca o gráfico de em unidades para esquerda;
Agora suponha que
- , expanda o gráfico de verticalmente por um fator de ;
- , reflita o gráfico de em torno do eixo
Abaixo temos um gráfico que também vai nos ajudar a visualizar o que ocorre:
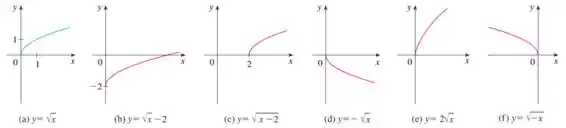
Com essas orientações a gente vai conseguir resolver essa atividade.
Passo 2
- Para obter o gráfico de , temos que alongar o gráfico de na vertical, multiplicando por um fator . Assim, teremos que cada par ordenado do nosso novo gráfico será dado por , por exemplo.
- Quando subtraímos algum valor dentro do argumento da função, teremos um deslocamento do gráfico para a direita. Logo, o gráfico dessa função ficará unidades para a direita com relação à .
- Quando multiplicamos por , estamos fazendo com que todos os valores de que estavam acima do eixo fiquem negativos, enquanto todos os valores que estavam abaixo do eixo fiquem positivos. Sendo assim, a nossa função vai ficar refletida com relação ao eixo .
- Para conseguir o gráfico de , temos que fazer o que dito no item (a) e (b): primeiro nós iriamos alongar na horizontal o gráfico de por um fator e, depois, iriamos refletir ele em torno do eixo , beleza? Ah, e pode fazer isso em qualquer ordem que vai dar a mesma coisa ;)
- Quando multiplicamos ou dividimos por um número dentro do argumento da função, estamos alterando o comportamento de seu gráfico na horizontal: a multiplicação faz com que o gráfico fique mais encolhido, enquanto a divisão faz com que ele se expanda. Nesse caso, o nosso gráfico de vai ficar mais comprimido na horizontal por um fator com relação à .
- Para descobrirmos quem vai ser esse cara, iremos primeiro fazer a mesma coisa que fizemos em (a): expandir o gráfico na vertical por um fator . Depois disso, iremos deslocar ele na vertical – é o que acontece quando somamos ou subtraímos um valor de , beleza? Como estamos subtraindo, além dessa expansão, o gráfico vai ficar deslocado unidade para baixo.
Passo 3
Passo 4
Resposta
- Expanda na vertical por um fator .
- Desloque para a direita em unidades.
- Reflita com relação ao eixo .
- Expanda por um fator na vertical e, em seguida, reflita com relação ao eixo .
- Comprima na horizontal por um fator .
- Expanda na vertical por um fator e, em seguida desloque ele para baixo em unidades.
Exercícios de Livros Relacionados
Crie uma equação para o gráfico da função a seguir, comprimido verticalmente por um fator de 2. y = 1 + 1 x ² ²
Crie uma equação para o gráfico da função a seguir, alongado horizontalmente por um fator de 3. y = 1 + 1 x ² ²
Crie uma equação para o gráfico da função a seguir, alongado horizontalmente por um fator de 2. y =1 - x ³ ³
Faça o gráfico da função:y = (1)/(x ²) - 1 ²
Faça o gráfico da função: y = x - 1 3 + 2 Comece pelo gráfico de uma das funções padrão apresentadas nas figuras 1.14-1.17 e aplique a mudança adequada.