Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.4 - Ex. 17

Expresse o integrante como soma de frações parciais e calcule a integral:

∫ 0 1 x 3 d x x 2 + 2 x + 1

Passo 1

Para solucionar uma integral por expansão de frações parciais, temos que separar os denominadores como funções de primeiro grau e em seguida descobrir quais numeradores satisfazem essas novas frações.

Feito isso, dividimos em integrais distintas e solucionamos usando as propriedades de logaritmo natural l n , obtendo nossa solução.

Por fim substituiremos os limites de integração.

Passo 2

Fazendo a divisão polinomial, teremos:

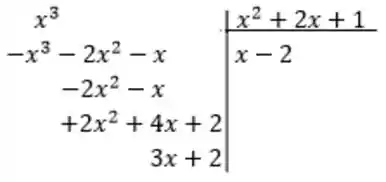
Reescrevendo a fração original como a divisão polinomial, teremos:

∫ 0 1 3 x + 2 x 2 + 2 x + 1 + x - 2 d x

Separando a integral, temos:

∫ 0 1 3 x + 2 x + 1 2 d x + ∫ 0 1 x - 2 d x

Como escrever por meio de frações parciais é uma forma de fatoração, torna-se mais simples fatorar o numerador da equação da esquerda e simplifica-la.

∫ 0 1 3 2 2 x + 2 - 1 x + 1 2 d x + ∫ 0 1 ( x - 2 ) d x

Simplificando, teremos:

∫ 0 1 3 2 x + 1 2 x + 1 x + 1 - 1 x + 1 2 d x + ∫ 0 1 x   d x - 2 ∫ 0 1 1   d x

∫ 0 1 3 x + 1 d x - ∫ 0 1 1 x + 1 2   d x + ∫ 0 1 x   d x - 2 ∫ 0 1 d x

Passo 3

Integrando, conhecendo as primitivas, teremos:

3 ln ⁡ x + 1 + 1 x + 1 + x 2 2 - 2 x 0 1

3 ln ⁡ 1 + 1 + 1 1 + 1 + 1 2 2 - 2 × 1 - 3 ln ⁡ 0 + 1 + 1 0 + 1 + 0 2 2 - 2 × 0

3 ln ⁡ 2 + 1 2 + 1 2 - 2 - [ 1 ]

3 ln ⁡ ( 2 ) + 1 - 2 - 1

3 ln ⁡ 2 - 2

Resposta

3 ln ⁡ 2 - 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Escreva as formas de decomposição em frações parcias da função (como no Exemplo 7 ). Não determine os valores numéricos dos coeficientes. x 3 x 2 + 4 x + 3 2 x + 1 x - 1 3 x 2 + 4 2
Calcule a integral. ∫ a x x 2 - b x d x
Escreva as formas de decomposição em frações parcias da função (como no Exemplo 7 ). Não determine os valores numéricos dos coeficientes. x 4 x 3 + x x 2 - x + 3 1 x 6 - x 3
Calcule a integral. ∫ 2 3 1 x 2 - 1 d x
Calcule a integral. ∫ 1 x + a x + b d x