Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 7.4 - Ex. 4
Escreva as formas de decomposição em frações parcias da função (como no Exemplo ). Não determine os valores numéricos dos coeficientes.
Passo 1
- Como o grau do numerador é maior que o grau do denominador, vamos dividir os dois:
- Aqui temos o Caso I e o Caso III, onde o denominador é um produto de fatores lineares distintos, e onde contém fatores quadráticos irredutíveis sem repetição, vamos usar a fórmula então:
Dividindo por vamos ter um quociente e resto , assim:
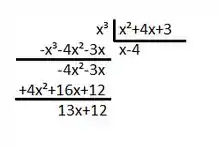
Agora vamos fatorar o denominador, achando as raízes de temos:
Usando Bhaskara:
Temos então:
Assim ficamos com:
Aqui temos o Caso I, onde o denominador é um produto de fatores lineares sem repetição , vamos usar a fórmula então:
Passo 2
Resposta
Exercícios de Livros Relacionados
Escreva as formas de decomposição em frações parciais da função (como no exemplo 7). Não determine os valores númericos dos coeficientes. 5 .a x 4 x 4 - 1b t 4 + t 2 + 1 t 2 + 1 t 2 + 4 2
Faça uma substituição para expressar o integrando como função racional e então calcule a integral ∫ e 2 x e 2 x + 3 e x + 2 d x
Escreva as formas de decomposição em frações parciais da função (como no exemplo 7). Não determine os valores númericos dos coeficientes. 1 .a2 x ( x + 3 ) ( 3 x + 1 )b 1 x 3 + 2 x 2 + x
Calcule a integral. ∫ 3 4 x 3 - 2 x 2 - 4 x 3 + 2 x 2 d x
Nos exercícios de 1 a 62, calcule a integral indefinida. 32 .∫ d x x ln x( ln x - 1 )