Faça um esboço da função cotangente hiperbólica. Ache as equações das assíntotas.
Passo 1
Para montarmos esse esboço bem detalhado, temos que fazer o seguinte passo a passo:
Ache as assíntotas horizontal e vertical do gráfico de ;
Os extremos relativos de ;
Os pontos de inflexão do gráfico de ;
Os intervalos em que é crescente
Os intervalos em que é decrescente;
Onde o gráfico é côncavo para cima;
Onde o gráfico é côncavo para baixo;
Vamos seguir essa lógica então para
Lembrando que:
Passo 2
Vamos para as assíntotas:
Vamos começar pela assíntota horizontal.
Assíntota horizontal: fazer o limite no infinito. Ou seja,
Passo 3
Agora vamos aos limites.
Vai ficar:
Deu uma indeterminação, vamos dar uma lgebrizada ai para tentar resolver:
Voltando para o limite:
Temos uam assíntota horizontal em
Passo 4
Agora vamos aos limites.
Vai ficar:
Opa, indetemirnação. Vamos usar L’Hospital para sair dessa
Temos uam assíntota horizontal em
Passo 5
Vamos para as verticais. Para isso, temos que procurar algum valor de que faça o limite ir para . Normalmente procuramos quando o denominador da fração for . Aqui, temos uma potencia racional, que é uma fração na potência. Nesses casos não teremos assíntotas verticais porque a soma de exponencial não vai ser nunca
Passo 6
Vamos aos extremos e os intervalos de crescimento e decrescimento. Para isso temos que analisar o sinal de .
Como:
Vamos ter
Esse termo é positivo paras qualquer valor de , então:
A função é crescente se e decrescente se , então:
Passo 7
Agora vamos ver os extremos. Pelo teste da primeira derivada, teremos máximo quando a função vai de crescente para decrescente, e mínimo quando a função for de decrescente para crescente.
Como a função e sempre crescente, não teremos extremos.
Passo 8
Vamos agora para a concavidade e os pontos de inflexão. A função é côncava para cima se e côncava para baixo se .
O ponto vai ser de inflexão quando muda a concavidade.
Vamos pegar
Derivando
A secante hiperbólica é sempre positiva.
Vmaos olhar o sinal da tangente.
Vamos ter que a derivada vai depende do sinal de
Vamos ter
Então:
Isso também nos diz que é um ponto de inflexao
Passo 9
Para terminar vamos ao esboço. Para isso, precisamos juntar todas as informações.
Assíntotas horizontais:
Ponto de inflexão:
O gráfico vai ficar:
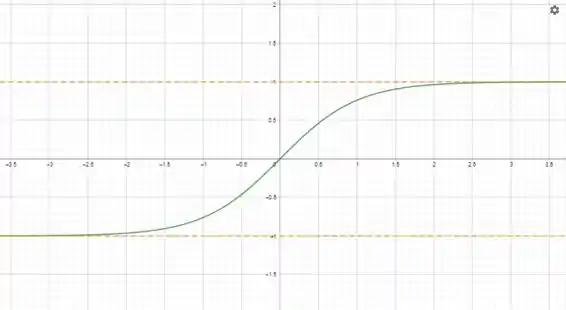
Resposta